Reference no: EM131097532

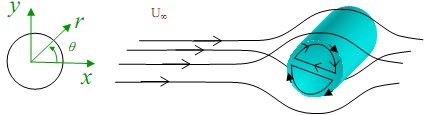
Question 1. Consider a trapped, cylindrical liquid bubble (viscosity µ₂ ) in a flow field of another liquid (viscosity µ1), as shown below. Assume that the bubble is an infinitely long cylinder. The pressure is not radially deformable. However, as liquid flows around it, the interface moves giving rise to circulation within the bubble. V_θ at bubble interface r = R is given by V_θ =f_(R)f_(θ).

You are required to find this interface velocity and the velocity components around the bubble using a stream function approach. This is a creeping flow problem.

a) Write down all the appropriate velocity boundary conditions for the flow around the bubble (one of the BCs may not be known explicitly). Determine an appropriate form for the stream function ψ(r,θ) for use in part b).

b) Obtain a general expression for ψ(r,θ). You do not have to evaluate the constants of your expression for this part.

c) Use boundary conditions to determine ψ(r,θ) and the velocity components explicitly for the flow around the bubble. Determine whatf (R)f (θ) are for Vθ =f (R)f (θ) at r = R.

d) If you were to solve the flow field of the liquid within the bubble, what boundary conditions would you have used to obtain V_r and V_θ. Mention only three BCs.

Question 2. A small spherical gas bubble of radius R is slowly rising with a velocity U_∞ in an incompressible Newtonian fluid (density ρ, viscosity µ). The fluid is at rest far from the bubble. Unfortunately, the liquid is also radially drawn into the gas bubble so that your radial velocity at r = R is given by Vr = f (R) f (θ). For simplicity, assume a) the bubble not to be deformable, b) the inside gas not to be circulating and no slip boundary condition to hold for the tangential velocity component, c) viscosity of gas to be very small, d) the radial velocity at bubble surface does not affect velocities at large distances from the sphere, e) moving of liquid into bubble causes no change in bubble properties.

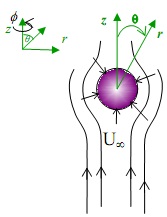
You are required to find the velocity field for the flow around the sphere. Assume that R does not change and the bubble is still incompressible for your calculations, and creeping flow.

a) Determine an appropriate form of the stream function ψ(r,θ).

Your answer in this part can have unknown constants such as A, B, C, etc. U∞

b) Obtain expressions for ψ_(r,θ) in terms of known parameters. Mention the boundary conditions used.

c) What is f_(θ),f_(R) for V_(r) at the sphere radius?

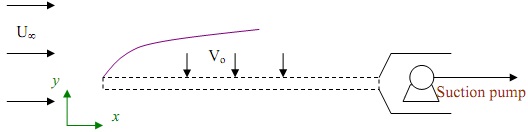
Question 3. Suction through Moving, Perforated Plate: Steel plates with holes are made by continually generating sheets from a die and move with a velocity U_p, as shown below. The entire set up in this case, however, lies in a bath of moving oil, which has a velocity U∞ as shown.

Further, a pump is producing suction of the fluid through the plate holes, the magnitude of the suction velocity being given by Vo. It is of importance to calculate the boundary layer at the leading edge of the plate.

(a) Calculate vx within the boundary layer. Mention reference frame and all boundary conditions. Assume a velocity profile of the form:

v_x = A cos (B + Cy/δ), where A,B, C are constants that need to determined.

(b) Determine an expression for the integral boundary layer equation for this problem. (Use the equation of motion, continuity equation, etc, as shown in class).

(c) Determine an expression for δ(x) using the integral boundary layer equation. In solving for δ(x) you may assume U_∞ / V_o >>1.

(d) From a processing standpoint, it is desirable to remove the boundary layer. Do you think it is possible to eliminate the boundary layer under any conditions (e.g. changing U_p, U_∞, etc.)?

Be explicit in your response.

Question 4. Ideal Flow around a cylinder: Consider an ideal flow past a long cylinder of radius R. As shown, the cylinder is assumed to be aligned in the z direction, and far away there is a velocity U in the x direction.

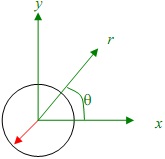
(a) Calculate the potential function for this flow using appropriate boundary conditions.

(b) Calculate the stream function for this flow.

(c) Obtain the velocity profile around x the cylinder using either (a) or (b).