Reference no: EM1318591

Question 1. Consider the relational schema

part(part-id, name, cost)

subpart(part-id, subpart-id, count)

A tuple (p1, p2, 3) in the subpart relation denotes that the part with part-id p2 is a direct subpart of

the part with part-id p1, and p1 has 3 copies of p2. Note that p2 may itself have further subparts.

Write a recursive SQL query that outputs the names of all subparts of the part with part-id "P-100".

Question 2. Consider the relation, r, shown below. Give the result of the following query:

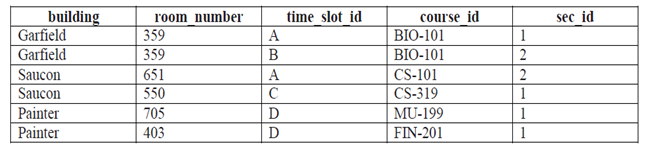
 SELECT building, room_number, time_slot_id, count(*)

FROM r

GROUP BY ROLLUP (building, room_number, time_slot_id)

Question 3. Consider an employee database with two relations

employee(employee-name, street, city)

works(employee-name, company-name, salary)

where the primary keys are underlined. Write a query to find companies whose employees earn a

higher salary, on average, than the average salary at "First Bank Corporation".

a. Using user defined SQL functions as appropriate.

b. Without using user defined SQL functions (you can use built-in SQL functions such as

avg(), min()).

Question 4. Write the following queries in both relational algebra and SQL, using the university schema.

(Appendix A, page 1271, look at that .zip file) Attachment:- DDL.zip

a. Find the names of all students who have taken at least one Comp. Sci. course.

b. Find the IDs and names of all students who have not taken any course offering before

Spring 2009.

c. For each department, find the maximum salary of instructors in that department. You

may assume that every department has at least one instructor.

d. Find the lowest, across all departments, of the per-department maximum salary

computed by the preceding query.

Question 5. Construct an E-R diagram for a hospital with a set of patients and a set of medical doctors.

Associate with each patient a log of the various tests and examinations conducted.

Question 6. Explain the distinction between disjoint and overlapping constraints.

Question 7. Explain the distinction between total and partial constraints.

Question 8. Consider the following set F of functional dependencies on the relation schema

r(A,B,C,D,E,F):

A --> BCD

BC --> DE

B --> D

D--> A

a. Compute B+.

b. Prove (using Armstrong's axioms) that AF is a superkey.

c. Compute a canonical cover for the above set of functional dependencies F; give each step

of your derivation with an explanation.

d. Give a 3NF decomposition of r based on the canonical cover.