Reference no: EM132170610

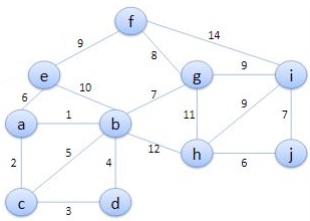
1. Using Dijkstra's Algorithm find the shortest path from a to c.

Write a pseudocode for implementing Dijkstra Algorithm.

2. Implement Prim's Algorithm on the below graph.

3. Min-Heap

Requirements

In this sub-project, you will implement one class:
1. A binary min-heap: QuaternaryMinHeap

Description

This class stores a fixed number of values in a binary minimum heap. If there are zero elements in the heap, the heap is said to be empty. The constructor is passed the capacity as an argument (defaulting to 10). The heap is to be implemented as is desribed in the course notes.

Member Variables
Use whatever member variables you feel are necessary.
Member Functions

Constructors

BinaryMinHeap( int = 10 )

This allocates enough memory for a heap capable of storing n
objects.

Destructor

Any memory you allocated must be cleaned up. (O(1))
Copy Constructor

Create a copy of the object. (O(1))
Assignment Operator =

Assign the heap to be an exact copy, in all respects, of the argument. (O(nrhs))
Accessors

This class has seven accessors: int size() const;
Returns the number of items in the heap. (O(1)) int capacity() const;
Returns the number of items which can be stored in the heap. (O(1))
bool empty() const;
Returns true if the heap is empty, false otherwise. (O(1)) bool full() const;
Returns true if the heap is full, false otherwise. (O(1)) Type head() const;
Retrieves the object stored in the front of the heap. This function throws a underflow if the heap is empty. (O(1))
Type retrieve( int n ) const;
Returns the object stored in the nth location of the array implementation of the heap. The argument will always be between 1 and size(). O(1)
bool member( Type const & ) const;
Returns true if the argument is stored in the heap and false otherwise. (O(n))

Mutators

This class has four mutators: void push_heap( Type const & );

This places the argument into the appropriate location in the heap as per the course notes and moves it up the heap as necessary. If the heap is full, throw an overflow exception. (O(ln(n)))
Type pop_heap();
Dequeue the minimum element from the heap and return it. The heap must be modified as described in course notes. Be sure to keep track of the last element in the array. (O(ln(n)))
bool remove( Type const & );
Remove the argument from the heap. You will have to perform a similar operation to pop_heap(), however, you will start at the location in the array where the object is removed. (O(n))
void clear();
Make the heap empty. (O(1)

4. You'll build a simple binary tree data structure from some arbitrary input.

1. Build a class Node. It should have a value that it stores and also links to its parent and children (if they exist). Build getters and setters for it (e.g. parent node, child node(s)).

2. Write a method build_tree which takes an array of data (e.g. [1, 7, 4, 23, 8, 9, 4, 3, 5, 7, 9, 67, 6345, 324]) and turns it into a binary tree full of Node objects appropriately placed. Start by assuming the array you get is sorted.

3. Now refactor your build_tree to handle data that isn't presorted and cannot be easily sorted prior to building the tree. You'll need to figure out how to add a node for each of the possible cases (e.g. if it's a leaf versus in the middle somewhere).

4. Write a simple script that runs build_tree so you can test it out.

5. Build a method breadth_first_search which takes a target value and returns the node at which it is located using the breadth first search technique.

6. Build a method depth_first_search which returns the node at which the target value is located using the depth first search technique. Use an array acting as a stack to do this.

7. Next, build a new method dfs_rec which runs a depth first search as before but this time, instead of using a stack, make this method recursive.