Reference no: EM133021075
Question 1. Let A be an m x n matrix with ij-th entries aij ∈ R. Let c1, ...,cn be real numbers, and x1, , xn be variables.
In each of the following examples, you are given an optimization problem. For each example, explain why the optimization problem is not a linear program, and find a trick to convert it to an equivalent linear program.
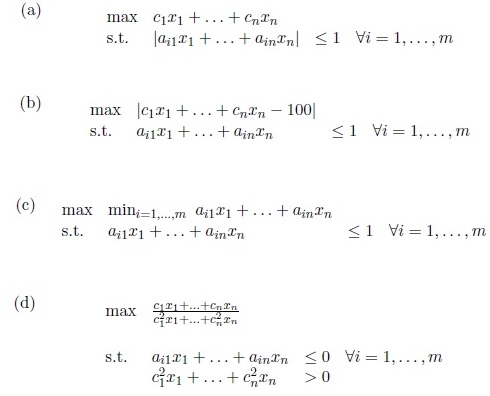
Question 2. Suppose that we want to find the "best" approximation of the function f(x) = x sin(x) by a degree 4 polynomial p(x) = ax4 + bx3 + cx2 + dx + e on all the integer points k ∈ [-10,10]. Here, the "best" means the following:
The error of such an approximation is the worst (meaning largest) difference If |(k)-p(k)| among integers -10 ≤ k ≤ 10. We want to find the approximation with the smallest error.
Write a linear program that solves this problem. How many constraints are there in your linear program?
Question 3. Recall that a colouring is called proper if it does not assign the same colour to any pair of neighbouring vertices, and 3COL is the problem of deciding whether a graph is 3-colourable. Let X be the following problem.
• Input: An undirected graph G.
• Question: Does G have a proper 3-colouring that assigns red to more than 99% of the vertices?
Prove that 3COL ≤p X (that is, 3COL is polynomially reducible to X) by giving an efficient algorithm that solves 3COL using a black-box algorithm for X.
Question 4. Recall that Hamiltonian Cycle problem is defined as follows:
• Input: An undirected graph G.
• Question: Is G Hamiltonian (meaning that it contains a cycle that visits all the vertices)? Let X be the following problem:
• Input: An undirected graph G, and an integer k ≥ 0.
• Question: Can G be made Hamiltonian by adding at most k edges to it?
First prove that X NP. Then prove that Hamiltonian Cycle ≤p X.
Question 5. Prove that Hamiltonian Cycle ≤p Y, where Y is the following problem:
• Input: An undirected graph G.
• Question: Does G have two cycles that do not share any vertices, and together include all the vertices of G?