Reference no: EM13271
In this game, we have a number of players interacting in a simple way. The game takes place on a (virtual), two-dimensional piece of land. There are two types of player: Sheep, and Wolves. Sheep start at one point of the land, and they have to get to get to a green pasture to win. They move one step at a time. Usually, there are several sheep that start out at the same time. The more sheep get to the destination, the better. This diagram shows five sheep ("s") and the green pasture at the top:
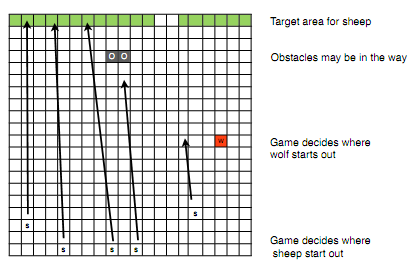
Unfortunately, there is also a wolf. The wolf's objective is to find (and eat) as many sheep as possible. The wolf may be a little faster than the sheep, but it always needs a number of steps to finish eating one.Sheep and wolves are realized as separate Java classes. Each student will submit either a Sheep or a Wolf class. We're going to play a tournament: we're going to have an instance of each wolf and instances of four or five different sheep play the game and tally up the results.
Beware... the rules of the game are simple, but its dynamics can be very complex.
Example: Suppose we have 30 students (numbered 0..29) in this class. We will form 7 teams (A,B,C,D,E,F,G). Teams A,B,C,D will write the sheep - this means we'll have about 16 Sheep classes coming in. Teams E,F,G will write wolves - which makes another 14 Wolf classes.
In the tournament, we'll run many thousand games, each with one combination of the sheep classes from one of the four sheep teams, and exactly one wolf (out of 14) - that's 56 combinations. We need three rules of engagement to make this work.
Rule 1: You may not collaborate with other students outside of the team.
Rule 2: You should collaborate with the other students within your team. While everyone has to do their own implementation, you, for
example may collude to plot joint strategies against the wolf (if you're programming a sheep agent).
Rule 3: You must submit only your own code and may not write code for others. Small, shared functions that are marked as such are OK.
The playing field is a m by n rectangular grid with m*n cells. In each game, there are a number of players (several sheep players, and one wolf). Each player occupies exactly one cell in the grid, and no cell will contain more than one player (except a combination of the wolf and a sheep). Cells may also contain an obstacle, in which case no player can occupy the cell.
Players start at an assigned location. There are multiple steps (iterations): In each iteration, each sheep may move exactly one step to the left, the right, up, down, or diagonally, but not beyond the boundaries of the grid. In each iteration, the wolf may also move a constant k steps (k is to be determined by the game, and fixed throughout the tournament. All players will be told k). All players make one move at a time and see the updated positions. The wolf moves last. The player instance determines a move and communicates it as Δx and Δy (steps in each direction), where Δx and Δy are signed integers. For sheep, (Δx2 + Δy2) <= 2.0. For the wolf, (Δx2 + Δy2) < k2. For instance, if the wolf decides to move 2 steps to the left (Δx=-2) and 3 steps up (Δy=-3), then that would be a legal move if k is at least 2.9, because:
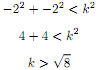
If more than one sheep try to occupy the same cell, one of the sheep's moves fails and the sheep will not move. If the wolf and a sheep attempt to occupy the same location, the wolf begins to eat the sheep. A meal takes a number of steps f, during which the wolf will not move. The sheep perishes. Several green pastures ("goal cells") are determined by the game. Their location is known to all players. If a sheep reaches one these pastures, the sheep wins its game and disappears. The wolf cannot enter a pasture. The game terminates when all sheep have reached pastures or have been eaten, or after m+n steps, whichever comes first.
Parameters: The game parameters are available to the players upon instantiation:
