Reference no: EM131734267

Question: The following table gives the NPI total return for a three-year (12-quarter) period for Boston and San Francisco.

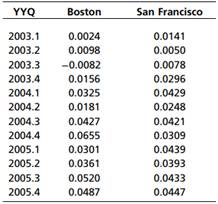
Compute the following quarterly statistics for both cities to the nearest basis point, and answer the subsequent questions.

a. The arithmetic average return (use the AVERAGE function in Excel)

b. The standard deviation of the return (‘‘volatility,'' use STDEV in Excel)

c. The geometric mean return (you can use the Excel statistical function GEOMEAN, but you have to add unity to each return in the series, and then subtract unity from the GEOMEAN result, or just apply the geometric mean return formula directly by compounding the returns in the spreadsheet)

d. Why are the arithmetic means higher than the geometric means?

e. Based on the geometric mean, and factoring up to a per-annum rate, by how many basis points did San Francisco beat Boston during this period?

f. Now compute the quarterly Sharpe ratio for each city based on the geometric mean you computed in (c) and the volatility you computed in (b). The Sharpe ratio is a measure of risk-adjusted return performance, defined as the risk premium divided by the volatility. Assume that the average quarterly return to Treasury Bonds during the period in question was 1.50%. Which city had the better Sharpe ratio?