Reference no: EM131006188

Homework:

Chapter deals with dimensionless groups, the most important of which in fluid mechanics is the Reynolds Number R_e = ρVL/μ, a measure of the ratio of inertial to viscous forces. The Re appears in most drag force relations and it determines when we pass from laminar to turbulent flow regimes - we use it a lot. You are expected to learn how to reduce a function of many variables ( e.g. V, P, L, A, t, ρ, μ, ω,...) to a function of a few dimensionless groups, called Pi groups, using the Buckingham method, and then how to use these dimensionless group relations to scale experiments and present data.

The recipe is straightforward: (1) Assume a given number of variables, N, which involve r dimensions (e.g. M, L, t), (2) of these N variables choose r repeating variables (in most cases r =3) which collectively contain all the relevant dimensions but no two of them have the same dimensions; (3) construct dimensionless groups, termed Pi (g) groups, by combining the repeating variables with each of the (N-r) remaining variables. It is a fast learn to do this and the type of results are very important in science to reduce the number of variables which must be studied in experiments. For example, if one supposes that the drag force F on a sphere of dimeter D in flowing fluid depends on the variables ρ, μ, L, V, this method can reduce five variables down to two dimensionless groups, showing that a dimensionless drag coefficient C_D = (F/A)/(1/2ρV²) for any sphere depends only on some function of Reynolds number, Re = ρVD/μ. We can then experimentally determine the universal relation CD = f(R_e), using only one fluid and one sphere, and varying only velocity. This result can then be applied to all fluids, at any density, and for any sphere. You can imagine the savings in experimental dollars this yields. Using then groups we can scale experiments and predict results. Section 7.11 summarizes a few of the most common dimensionless groups - you should look for these in your homework problems.

Section shows we can also render the fundamental equations (e.g. the N-S equation) dimensionless by defining dimensionless length, velocity, and time variables and thereby extract the same type of information about important dimensionless groups; the appropriate dimensionless groups become coefficients of the terms in the differential equations. This procedure can guide us in determining when to drop certain terms for certain flows. For example, a very low Re (highly viscous flows) suggests we can drop the inertial acceleration terms on the LIIS of the N-S equations. However, it is equally important to render the boundary conditions dimensionless in order to extract all important dimensionless groups for a particular flow.

1. Water is pumped around a 40 m long loop of pipe which is 2 cm in diameter . The viscous head losses are given by hL = K (V²/2g ), with a loss coefficient K = 25. The pump has a head (m) versus flow rate (m³/s) relation given by: h_p = 400 -10⁴ Q.

Find (a) the expected flow rate; (b) the required pump power; (c) AT of the water after one loop cycle? [hint: ΔU = CvΔT) ]; assume water C_v = 4.2 kJ/kg°K.

2. Consider fully developed laminar flow between two horizontal flat plates separated by a distance D, of flow length L driven by dP/dx < 0 . In a coordinate system shown with the flow in the x direction and y = 0 at the centerline:

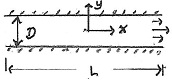
(a) Write down the appropriate N-S equations and boundary conditions and solve for u(y);

(b) solve for the average velocity V as a function of dp/dx = Δp/L;

(c) Assume the head loss is to be given in terms of a dimensionless "friction factor", f* , such that h_L ≡ (L/D) f*V²/2g. Compare your analytic solution for Δp to the Extended Bernoulli energy equation using h_L applied to this flow, and derive a relation between the friction factor f* and the Reynolds number R_eD ≡ ρVD/µ based on the plate separation D;

(d) compute the friction factor f* and the required Ap for a flow of an oil film ( SG = 1.2 ; µ. = 0.2 N.s/m²) between two plates 1 mm apart and 0.5m long at a speed of V = 10 cm/s

3. Fig 7.7 (pg 380) shows that a coefficient of drag C_D ≡ F/(1/2AρV²).for smooth spheres should only be a function of a Reynold's number, (Re a ρVD/µ.). Here F is the total drag force of the fluid on the sphere, and includes all the viscous and pressure forces. The drag on a large (D = 15 cm) sphere in air at V = 5 m/s is to be predicted using experimental results for a smaller sphere (D = 2 cm) in water.

(a) What water speed is required;

(b) what will be the ratio of drag forces (Fair/Fwater)?;

(c) for very small spheres it is known that CD = 24/Re.

What would be the ratio of terminal speeds (V₂/V₁) of very small rain drops falling through the air, one three times the size of the other, (D₂/D₁) = 3?

note: the terminal speed is reached when the drop weight equals the drag force ; air buoyancy force can be neglected.

4. For shallow liquids of depth D, the speed of a surface wave, V, is a function of p, g, and surface tension σ. Express the functional relation for wave speed as a function of depth in the simplest dimensionless form possible , using repeating variables ρ, g, σ.

5. An airplane wing is designed to move through air at a speed of V = 8 m/s. It has a span of S = 9 m and a chord length L = 1.5 m. The wing is to be tested using a small 1/10 th scaled model of the wing in water tunnel - keeping the ratio S/L fixed. The drag force F on the wing is given functionally by F = f ( ρ, µ , V, L, S).

(a) using the repeating variables ρ, V, L express the relation in 3 dimensionless Pi groups, Π₁ = f(Π₁, Π₂);

(b) what speed in the water tunnel is necessary for dynamic similarity?;

(c) what will be the ratio of forces Fmodel / Factual ?

6. A pump's power Ρ depends on rotational speed ω, flow rate Q, fluid density p, and impeller diameter D.

(a) Using repeating variables ρ, Q, D find dimensionless groups relating power to rotational speed.

(b) An oil (SG = 1.5) pump is to be designed to move 10 m³/s when running at 400 rpm. Testing is to be performed on a smaller 1:4 scale model running with Q = 1.0 m³/s, using water. To obtain dynamic similarity what should be the model rotational speed (rpm) ?

(c) If the small water model draws 200 W of power what will be the power requirement of the oil pump? Watch units.

7. The time, t, for a fluid to drain out of a viscosity calibration container depends on the orifice dimeter d, the fluid properties ti and p, and g.

(a) Using repeating variables ρ, g, d to derive two dimensionless groups which give t as a function of µ.

(b) An experiment using a orifice with d₁ = 2mm has determined that the drain time t is proportional µ³. For the same fluid what would be the ratio of times t₂/t₁ if the orifice diameter were doubled to d₂ = 4mm?