What values of x result in a local maximum

Reference no: EM131003723

1. Find all critical points and local extremes of each function on the given interval f(x)= x³ - 3x + 5 on the entire real number line .

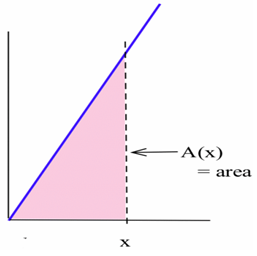
2. Define A(x) to be the area bounded by the t-axis, the line y = 2t and a vertical line at t = x.

(a) Find a formula for A(x)

(b) Determine A' (x)

1313_Area Bounded.png

3. The figure show the graph of the derivative of a continuous function f.

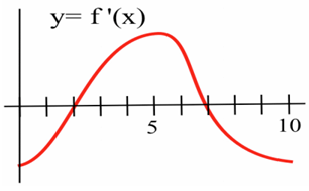
204_Graph of the derivative of a continuous function.png

(a) List the critical numbers of f.

(b) What values of x result in a local maximum?

4. A function and values of x so that f' (x) = 0 are given. Use the Second Derivative test to Determine whether each point (x, f (x)) is a local maximum, a local Minimum or neither.

h(x) x⁴ - 8x² - 2; x = -2, 0, 2.

Reference no: EM131003723

Questions Cloud

Describe friedman''s viewpoint towards csr and his policies : Describe Friedman's viewpoint towards CSR and his policies

The income tax benefit of the operating loss : Prepare the journal entry to recognize the income tax benefit of the operating loss.

What is the intensity of these waves : A local radio station transmits radio waves uniformly in all directions with a total power of 7.50 x 104 W. What is the intensity of these waves when they reach a receiving antenna located 20.0 km from the transmitting antenna?

Fiduciaries are associated with businesses : Fiduciaries are associated with businesses. Do you think that there is an argument that politicians could be or should be held as fiduciaries to the government.

What values of x result in a local maximum : The figure show the graph of the derivative of a continuous function f. What values of x result in a local maximum? What values of x result in a local minimum?

Prepare the journal entry to recognize the income tax : Prepare the journal entry to recognize the income tax benefit of the operating loss. AirParts elects the carry back option.

Most case both criminal and civil involve : Most case both criminal and civil involve: a. False misleading testimony b. Lawyers searching for the truth

Find the magnetic energy density in the same region : A long coaxial cable consists of two thin walled concentric conducting cylinders with radii a and b. The inner cylinder carries a current I (out of page) and the outer provides the return path for that current. The current creates a magnetic field..

Steve dies : 5. Steve dies a) any money he has will go to the state b) his property would go to cover probate costs

User Account

All Pages