Reference no: EM131021367

1. Which of the ordered pairs

(6, 1), (8, 0), (4, -2), (-4, 6)

are solutions for the equation x + 2y = 8?

2. A small company did a poll of how their employees commuted to work. The data is shown in the bar graph below.

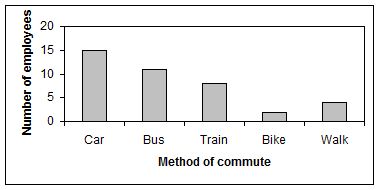
(a) How many people commute to work via car?

(b) How do most of the employees commute to work?

3. Complete the ordered pairs for the equation 2x + y = 10.

(5, ), ( , 10), ( , -2), (0, )

4. Find four solutions for the equation 3x + 5y = 15.

5. Graph 2x - y = 4.

6. Graph using the intercept method: x + 3y = 6.

7. Graph by first solving for y.

4x - 3y = 6

8. Graph using the intercept method: 2x + y = 4.

9. Find the slope of the line passing through the points (9, 12) and (8, 4).

10. Find the slope of the line passing through the points (-10, 10) and (0, 0).

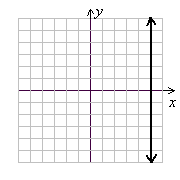
11. Find the slope of the graphed line.

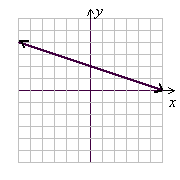
12. Find the slope of the graphed line.

13. If y varies directly with x, and y = 110 when x = 100, find the constant of variation k.

14. The following pie chart represents the results of a survey about whether people in a certain town have cats or dogs as pets.

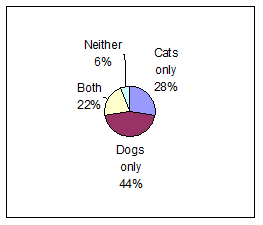
What percentage of the people have only cats or only dogs?

15. The line graph below shows the number of stray dogs in a certain city for the years listed.

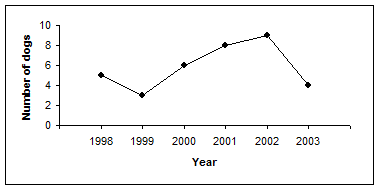
(a) Which year had the least amount of stray dogs?

(b) Between which two years did the greatest decrease in stray dogs occur?

16. A student earns $0.65 for each mistake she finds in a text. Sketch the equation of direct variation.

17. Find the slope and y-intercept.

8x + 5y = -50

18. Write the equation of the line with slope 4 and y-intercept (0, -5). Then graph the line.

19. Write the equation of the line with slope -1/2 and y-intercept (0, 3). Then graph the line.

20. A line passing through (10, 4) and (-3, y) is perpendicular to a line with slope -13/14. Find the value of y.

A) -13
B) -11
C) -10
D) -8

21. An airplane covered 15 miles of its route while decreasing its altitude by 31,000 feet. Find the slope of the airplane's line of descent. Round to the nearest hundredth. [Hint: 1 mi = 5280 feet.]

22. Determine which two equations represent parallel lines.

(a) y = (5/4) x + 3 (b) y = (4/5)x + 7 (c) y = (4/5)x - 7 (d) y = -(5/4)x + 7

23. Determine which two equations represent perpendicular lines.

(a) y = 9x - 9 (b) y = (1/9) x + 9 (c) y = -(i/9) x + 9 (d) y = (1/9) x - 9

24. Write the equation of the line that passes through point (0, -8) with a slope of (4/5).

25. Write the equation of the line passing through (6, 37) and (1, 12).