Reference no: EM13857961
Question 1:
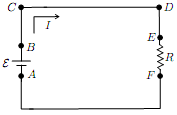
Consider an elementary circuit that consists of one battery of emf ε and a resistor of resistance R. Which of the following statements are true?
(a) The current flows from point A to B, this means that inside the battery the electric field points from the negative terminal to the positive terminal.
(b) There is a current flowing from point C to D, therefore there must be an electric field pointing from C to D even after equilibrium is reached.
(c) Inside the resistor there is an electric field pointing down to counteract the resistant force.
(d) The charge carriers gain energy from the battery, hence there must be a nonzero net force exerted on the charge carriers inside the battery even after equilibrium is reached.
(e) Point E has a higher electric potential than point F.
(f) Point A has a higher electric potential than point B.
(g) Point C has a higher electric potential than point D.
(h) The net electric potential energy gained and lost by the charge carriers is zero after traveling over a complete loop.
(i) The effective source force inside the battery that moves the charge carriers from one end to another is opposite to the static electric field inside the battery.
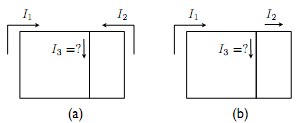
Question 2:
Suppose the current I1 and I2 is as that shown in the figure. Using the convention that all quantities I1, I2 and I3 are all positive, express I3 in terms of I1 and I2.
Question 3:
There are three resistors connected in series with a battery of emf ε. One could vary the resistance of the second resistor R2, while the resistance of the first and third one, R1 and R3 respectively, are fixed. Which of the following stamens are true?
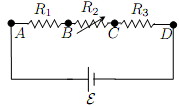
(a) As R2 increases, the net current flowing through the batter decreases.
(b) As R2 increases, the current flowing through R2 increases.
(c) As R2 increases, VBC increases, where VBC is the electric potential between point B and point C.
(d) As R2 increases, VAB and VCD increase as well.
(e) As R2 increases, VAD also increases.
(f) As R2 increases, the equivalent resistance seen by the battery increases.
Question 4:
Originally there were two resistors connected in parallel with a battery of emf E. We now add an additional resistor R in parallel with the original two as shown in the figure. Which of the following statements are true?
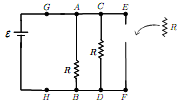
(a) After the change, the net current flowing through the batter decreases.
(b) After the change, the current flowing through AB increases.
(c) After the change, VEF increases, where VEF is the electric potential between point E and point F.
(d) After the change, VAB and VCD increase.
(e) After the change, VGH increases.
(f) After the change, the equivalent resistance seen by the battery, i.e. the equivalent resistance between G and H increases.
Question 5:
Originally there were three resistors connected in series with a battery of emf E. We now add an additional resistor R4 in parallel with R2 as shown in the figure. Which of the following statements are true?
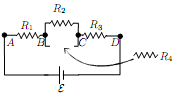
(a) After the change, the net current flowing through the batter decreases.
(b) After the change, the current flowing through R2 increases.
(c) After the change, VBC increases, where VBC is the electric potential between point B and point C.
(d) After the change, VAB and VCD increase.
(e) After the change, VAD increases.
(f) After the change, the equivalent resistance seen by the battery increases.
Question 6:
A circuit of identical light bulbs, each with the same resistance R except light bulb B4 which has a resistance 2R, is shown in the right figure. The two switches S1 and S2 are initially open. The battery has an emf E. Which of the following are true?
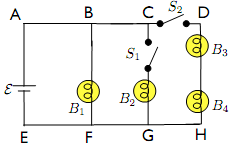
(a) The voltage across B1 will not change when we close either switch S1 or S2.
(b) The current through B1 will not change when we close either switch S1 or S2. We now close S1.
(c) The current at node B will split and therefore the current through B1 will decrease.
(d) The net current through the battery decreases because now the battery is connected with two resistors instead of one.
(e) The power supplied by the battery increases. We now close both S1 and S2.
(f) The current through B1 will decrease because now B1 is in series with B3 and B4.
(g) B3 and B4 are in series.
(h) Because B4 has larger resistance than B3, the current through B4 is smaller than that through B3.
(i) Because B4 has larger resistance than B3, the voltage across B4 is smaller than that across B3.
(j) The battery is in parallel with B1, B2 and the B3 + B4 line.
(k) Because B4 has larger resistance than B3, the voltage across B4 is larger than the voltage across B3.
(l) Nodes E, F, G, and H have the same electric potential regardless the switches are closed or not.
(m) Nodes A, B, and C have the same electric potential regardless the switches are closed or not.
Question 7:
(1) With the switch closed for a long time, the total energy supplied by the is the total energy stored in the capacitor.
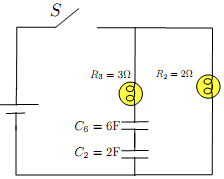
a) less than b) the same as c) greater than
(2) With the switch closed for a long tim, which stores more charge?
a) C6 b) C2 c) the same
(3) When the switch is opened, the time constant for discharging is
a) 40 sec b) 7.5 sec c) 9.6 sec d) 1.8 sec
Question 8:
Ampere-hour (Ah) is a unit of electric charge, equal to the charge transferred by a steady current of one ampere flowing for one hour, or 3600 coulombs. An AA rechargeable battery could have a capacity of 2,100 mAh. On the other hand, the battery of your laptop may have a capacity of 7,150 mAh.
(a) How many coulombs of charges could your laptop battery stores?
(b) Suppose your laptop charger has a power of 45W, and a voltage output of 15V. How much time does it take to charge your laptop from 0% to 100%?
Quantitative Problems
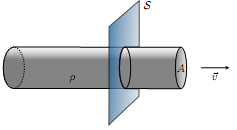
Problem 1
A long cylindrical rod with uniform volume charge density � and cross-sectional area A moving toward right with a velocity v→. It passes through an imaginary surface S perpendicularly. What is the current through S?
Problem 2
A hollow cylindrical resistor is made of a conducting material of resistivity �, length L, inner radius r1 and outer radius r2 as shown in Figure 1.
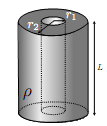

(a) Assuming that the current passes along the direction of the symmetry axis of the resistor, calculate the resistance R.
(b) The same voltage V is applied at the two ends of two solid thick conducting cylinders (see Figure 2) made of the same material of resistivity � such that the currents flow along the same direction as the symmetry axis. If one conductor is twice as long and twice the diameter of the second, what is the ratio of the current through the first relative to the second?
(c) The wiring of a house must be thick enough to prevent any fire hazard. What should the diameter D of a solid cylindrical
wire be if it is to carry a maximum current I and produce power losses of no more than P per meter of length?
(d) Recalculate the resistance R of the hollow cylindrical resistor pictured in Figure 1, now assuming that the current is radial .
Problem 3
Two concentric metal spherical shells, of radius a and b, respectively, are separated by weakly conducting material of conductivity �.
What is the resistance between the shells if the current flows radially?
Problem 4
Consider the circuit in the right figure.
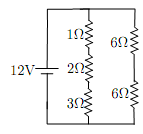
(a) What is the voltage across the 1-resistor?
(b) What is the current flowing through the 6 resistor?
Problem 5:
Consider the circuit in the right figure.
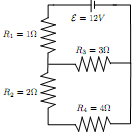
(a) What is the total power supplied by the battery?
(b) What is the power consumed by R4?
Problem 6:
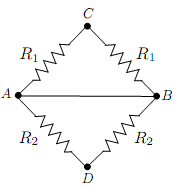
(a) What is the equivalent resistance between points A and B (the left and right nodes) in the given combination of resistors? In other words:
we could connect this combination to other circuit components by attaching one wire at A and another at B. The combination would then
have an equivalent resistance.
(b) What is the equivalent resistance between points C and D (the top and bottom nodes) in the given combination of resistors? There is a way to do this problem with a long calculation, or a short and fairly simple one { though if you do the short calculation, make sure you justify your reasoning.
Problem 7:
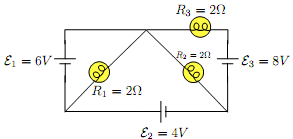
(a) Find the power supplied by battery 1.
(b) Now, if Battery 2 is replaced with a straight wire:
(I) R1 and R2 are in (a) series (b) paralle both (d) neither
(II) Brightness of bulb R1 (a) Increases (b) Decreases (c) Stays the same
(III) Brightness of bulb R3 (a) Increases (b) Decreases (c) Stays the same
Problem 8:
Four capacitors are arranged in the square shown below with C2 = 3F. It can be connected to a voltage supply, V = 10V, in the two different ways shown in Configuration A and Configuration B, below.
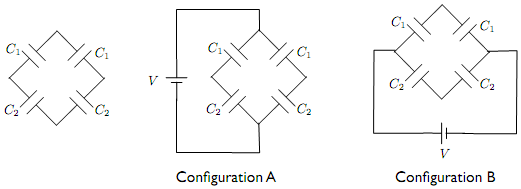
(a) You are told that CEqACEqB = 6F2, where CEqA is the equivalent capacitance of Configuration A, and CEqB is the equivalent capacitance of Configuration B. What is C1
(b) Calculate the energy stored in Configuration A, UA, and the energy stored in Configuration B, UB. Which configuration stores more energy?
Problem 9:
Consider the circuit shown below. The two switch A and B are original open. At t = T1, we close both switches. A long time after t = T1, we reopen switch A at t = T2 but with switch B remain closed. Please answer the following questions:
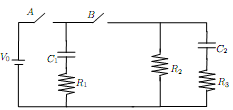
(a) What is the current through R1 right after T1?
(b) What is the current through R2 right after T1?
(c) What is the current through R1 right before T2?
(d) What is the current through R2 right before T2?
(e) What is the current through R2 right after T2?
(f) What is the current through R2 a long time after T2?
(g) How much charges have flowed through R2 from t = T2 to t = 1?
Problem 10:
Consider the circuit shown in the right figure. The switch is closed at t = 0.
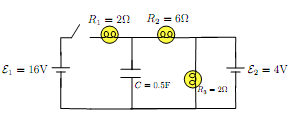
(a) Will the current flowing through R3 change over time? If so, what is its value right after and long after the switch is closed? If not, find its value after the switch is closed.
(b) Right after the switch is closed, what is the current through the capacitor? What is the voltage across it?
(c) Right after the switch is closed, what is the current through R2?
(d) Right after the switch is closed, what is the current through R1?
(e) Long time after the switch is closed, what is the current through R2?
(f) Long time after the switch is closed, what is the current through R1?
(g) Long time after the switch is closed, does the second battery E2 supply or consume energy?
Problem 11:
At t < 0 the voltage on capacitor C1 is V0, and the voltage across capacitor C2 is zero. At t = 0, the switch is closed.
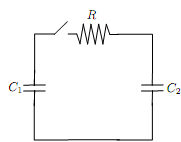
(a) After a long time, what is the charge on C2?
(b) After a long time, what is the total amount of heat energy deposited in resistor R? Hint: there is no need to use a differential equation to solve this problem, or to use any of the formulas for power in a resistor.