Reference no: EM132354546

Math Questions -

Q1. Find the value of the following improper integrals, or determine that the integral diverges.

(a) ₄∫^∞12/x^5/2 dx

(b) ₀∫¹2/x⁵ dx

Q2. Evaluate ₀∫^π/2 sin²xcos²x dx.

Q3. Let R be the region bounded by the graphs of y = √(2x), y = -x + 4 and the x-axis. Sketch this region and find the area of the region R.

Q4. Evaluate the following integrals:

(a) ₀∫³x/√(36-x²) dx

(b) ₀∫¹(-5x+2)/(3x²+13x+4) dx (Use Partial Fractions)

(c) ₀∫¹4z²/(1+z²)² dz (Use Trigonometric Substitution)

(d) ∫x(In x)² dx (Use Integration by Parts)

Q5. Determine if the following sequences converge. Note that these are sequences, so it is not appropriate to apply a test for convergence of a series. If the sequence converges, determine its limit.

(a) a_n = (n+1)/(2n²+3n+1), n ≥ 1

(b) b_n = (-1)ⁿ/(3n+2), n ≥ 1

(c) c_n = (2n²-n)/(4n²+3n+1), n ≥ 1

(d) d_n = ((5n+4)/5n)ⁿ, n ≥ 1

(Be careful; the sequence converges and its limit is not = 1)

Q6. Provide the first 10 terms of each of the following recursively defined sequences:

(a) a₁ = 1, a₂ = 1, a_n = a_n-1 +a_n-2 for n ≥ 3 (The Fibonacci Sequence).

(b) a₁ = 512, a_n = ½a_n-1 for n ≥ 2  (Geometric Sequence with ratio = ½).

Q7. Compute the arc length of the curve in the 2-dimensional plane described by y = ln (cos x), 0 ≤ x ≤ π/3.

Q8. Compute the surface area of the paraboloid obtained by revolving the curve y = √(2x), 0 ≤ x ≤ 4, about the x-axis.

Q9. Find the interval of convergence of each of the following power series:

(a) _n=1∑^∞(-1)ⁿ(x-4)ⁿ/5²ⁿ⁺¹

(b) _n=1∑^∞(x+3)ⁿ/n!

(c) _n=1∑^∞(-1)ⁿ(x+3)ⁿ

Q10. Consider the polar curves r = 3 - 3cos θ and r = 3.

(a) Sketch and shade the region inside both r = 3 - 3cos θ and r = 3.

(b) Determine the area of the region described in (a).

Q11. Find the surface area of the solid generated by rotating the curve c(t) = (t², t), 0 ≤ t ≤ 1 about the x-axis.

Q12. Suppose that at tank contains 100 gallons of water. Water starts flowing in at the rate of 40/(1+t) gal/min, and flowing out at the rate of 5 gal/min.

(a) Set up and solve a differential equation for V.

(b) Find the maximum for V.

(c) Using the graph, estimate when the tank will be empty.

Q13. Suppose that a donor leaves $500,000 to a charity, in an endowment account that yields interest at the annual rate of 4% compounded continuously. The charity will continuously draw $30,000 per year.

(a) Set up and solve a differential equation for the balance in the endowment after t years.

(b) How much will be left in the endowment after 10 years?

(c) How long will the endowment last? That is, how long will it take for the balance to be zero?

Q14. Recall Newton's Law of Cooling. The rate of change in the temperature of an object is proportional to the difference between the temperature of the object and the temperature of the surrounding medium. That is, if y represents the temperature of the object and T₀ is the temperature of the surrounding medium (also called the ambient temperature), then dy/dt = -k(y - T₀). This equation has the general solution y = T₀ + Ce^-kt, k is called the "cooling constant."

A hot object is submerged in a water bath whose temperature is 15^oC. The object cools from 100^oC to 50^oC in 90 seconds. In a different water bath, the same cooling occurs in 70 seconds. What is the temperature of the second bath?

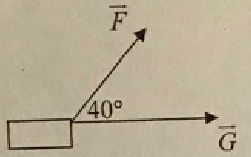
Q15. Find the resultant of the forces F^→, G^→, if the force F^→ has a magnitude of 80 lbs, the force G^→ has a magnitude of 100 lbs, G^→ acts in the positive horizontal direction, and F^→ acts at an angle of 40^o. You need to determine the magnitude and the direction of the resultant.

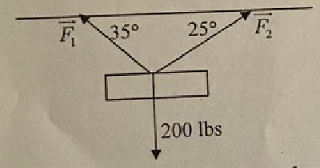
Q16. Find the tensions on the cables that hold a crate that weighs 200 lbs in equilibrium, as shown below.

Q17. For the vectors u^→ = (6, 1, -2), v^→ =(1, 4, 3). Determine:

(a) |u^→| and |v^→|

(b) u^→• v^→

(c) The angle between u^→ and v^→ (in degrees).

(d) u^→ x v^→

(e) The area of the parallelogram spanned by u^→ and v^→.