Reference no: EM13799657

Question 1- Starting from rest and rotating at constant angular acceleration, a disk takes 10 revolutions to reach an angular speed ω. How many additional revolutions at the same angular acceleration are required for it to reach an angular speed of 2ω?

Question 2- You are looking down from above at a merry-go-round and observe that it is rotating counterclockwise and that its rotation rate is slowing. If we designate counterclockwise as positive, what is the sign of the angular acceleration?

Question 3- A wheel of radius R and angular speed ω is rolling without slipping toward the north on a flat, stationary surface. The velocity of the point on the rim that is (momentarily) in contact with the surface is (a) equal in magnitude to Rω and directed toward the north, (b) equal to in magnitude Rω and directed toward the south, (c) zero, (d) equal to the speed of the center of mass and directed toward the north, (e) equal to the speed of the center of mass and directed toward the south.

Question 4- A perfectly rigid ball rolls without slipping along a perfectly rigid horizontal plane. Show that the frictional force acting on the ball must be zero. Hint: Consider a possible direction for the action of the frictional force and what effects such a force would have on the velocity of the center of mass and on the angular velocity.

Question 5- A 12-cm-radius disk that begins to rotate about its axis at t = 0, rotates with a constant angular acceleration of 8.0 rad/s². At t = 5.0 s, (a) what is the angular speed of the disk, and (b) what are the tangential and centripetal components of the acceleration of a point on the edge of the disk?

Question 6- A wheel rotates through 5.0 rad in 2.8 s as it is brought to rest with constant angular acceleration. Determine the wheel s initial angular speed before braking began.

Question 7- The tape in a standard VHS videotape cassette has a total length of 246 m, which is enough for the tape to play for 2.0.h (Figure). As the tape starts, the full reel has a 45-mm outer radius and a 12-mm inner radius. At some point during the play, both reels have the same angular speed. Calculate this angular speed in radians per second and in revolutions per minute.

Question 8- To start a lawn mower, you must pull on a rope wound around the perimeter of a flywheel. After you pull the rope for 0.95 s, the flywheel is rotating at 4.5 revolutions per second, at which point the rope disengages. This attempt at starting the mower does not work, however, and the flywheel slows, coming to rest 0.24 s after the disengagement. Assume constant acceleration during both spin-up and spin-down. (a) Determine the average angular acceleration during the 4.5-s spin-up and again during the 024-s spin-down. (b) What is the maximum angular speed reached by the flywheel? (c) Determine the ratio of the number of revolutions made during spin-up to the number made during spin-down.

Question 9- Determine the moment of inertia of a uniform solid sphere of mass M and radius R about an axis that is tangent to the surface of the sphere.

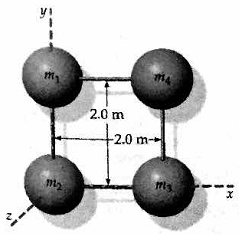
Question 10- Four particles, one at each of the four corners of a square with 2.0-m-long edges, are connected by mass less rods. The masses of the particles are m₁ = m₃ = 3.0 kg and m₂ = m₄ = 4.0 kg. Find the moment of inertia of the system about the z axis.

Question 11- A grinding wheel is initially at rest. A constant external torque of 50.0 Nm is applied to the wheel for 20.0 s, giving the wheel an angular speed of 600 rev/min. The external torque is then removed, and the wheel comes to rest 120 s later. Find (a) the moment of inertia of the wheel, and (b) the frictional torque, which is assumed to be constant.

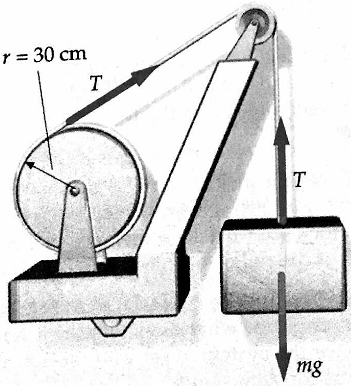
Question 12- A 2000-kg block is lifted at a constant speed of 8.0 cm/s by a steel cable that passes over a mass less pulley to a motor-driven winch. The radius of the winch drum is 30 cm. (a) What is the tension in the cable? (b) What torque does the cable exert on the winch drum? (c) What is the angular speed of the winch drum? (d) What power must be developed by the motor to drive the winch drum?

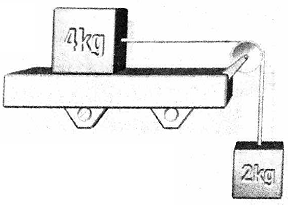
Question 13- The system shown in Figure consists of a 4.0-kg block resting on a frictionless horizontal ledge. This block is attached to a string that passes over a pulley, and the other end of the string is attached to a hanging 2.0-kg block. The pulley is a uniform disk of radius 8.0cm and mass 0.60 kg. Find the acceleration of each block and the tension in the string.

Question 14- A uniform cylinder of mass m₁ and radius R is pivoted on frictionless bearings. A mass less string wrapped around the cylinder is connected to a block of mass m₂ that is on a frictionless incline of angle θ as shown in Figure. The system is released from rest when the block is at a vertical distance h above the bottom of the incline. (a) What is the acceleration of the block? (b) What is the tension in the string? (c) What is the speed of the block as it reaches the bottom of the incline? (d) Evaluate your answers for the special case where θ = 90° and m₁ = 0. Are your answers what you would expect for this special case? Explain.

Question 15- An object is rolling without slipping. What percentage of its total kinetic energy is its translational kinetic energy if the object is (a) a uniform sphere, (b) a uniform cylinder, or (c) a hoop?

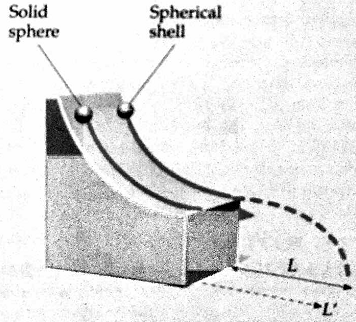
Question 16- Released from rest at the same height, a thin spherical shell and solid sphere of the same mass m and radius R roll without slipping down an incline through the same vertical drop H. Each is moving horizontally as it leaves the ramp. The spherical shell hits the ground a horizontal distance L from the end of the ramp and the solid sphere hits the ground a distance L' from the end of the ramp. Find the ratio L'/L.