Reference no: EM131457422
Question: Consider a transportation problem with two origins (warehouses) and three destinations (customers). The supplies at the warehouses are 60 and 80 units, respectively, while the demand is exactly 30, 50, and 40, respectively. The problem has been formulated as follows:
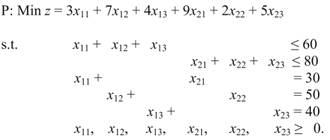
The printout is shown in Tables 2.37 and 2.38.
(a) What is the shipment plan and what are the associated costs?
(b) Which of the warehouses are fully used and which have still some units of the product in them (and how many)?
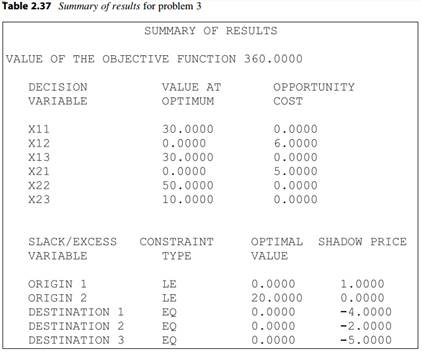

(c) What if the per-unit-cost of a shipment from origin 2 to destination 3 were to increase by $2, would that change the optimal solution? What if the cost were to decrease by $2?
(d) What would happen if the number of units available at the first warehouse were to be reduced by one unit? (Include cost considerations).
(e) What if we were offered extra units delivered to warehouse 2 at a rate of $2 per unit?
|
What is the best recommended course of action for client
: What potential effects would themes such as the client's culture, ethnicity, family, education, and gender have on the situation and recommendation(s)?
|
|
Constitute the majority of the report
: Prepare at least a 10 page research paper in 12 pt. font with double spacing Graphs, tables, text, and images may be included as part of the final research.
|
|
What is the purpose of the specialized interview
: What is the purpose of the specialized interview? How will you plan the assessment? Whom will you interview and why?
|
|
What should we buy and how much
: What should we buy and how much? How could you suggest that your new system would achieve any better levels of forecast accuracy?
|
|
What is the shipment plan and what are the associated costs
: Consider a transportation problem with two origins (warehouses) and three destinations (customers). The supplies at the warehouses are 60 and 80 units.
|
|
Human resources payroll information
: Answer the questions in straight to the point short answers. please answer them as they are numbered. shouldn't be more than 500 words
|
|
How many ways can you assign the ribbons
: You need to assign first, second, and third place ribbons. If there are 17 students who participated, how many ways can you assign the ribbons?
|
|
Describe the worst interface you have ever worked
: Describe the worst interface you have ever worked with and the best interface you have ever worked with.
|
|
Suppose a bipartite graph
: Suppose a bipartite graph has 20 vertices (two groups of n = 10) and 89 edges. Can we conclude that the graph has no perfect matching?
|