Reference no: EM1391974
Type A problems
A1. If p : X -> X* is surjective and X is a topological space, show that the collection T = {V ⊂= X*: p-1(V) is open in X} is a topology (that's the quotient topology).
A2. If p : X-> X* is surjective, show that the quotient topology on X* is the finest topology for which p is continuous. That is, if T is any topology on X* in which p is continuous, then T is contained in the quotient topology.
A3. Give an example of a Hausdorff space X and a surjective map p : X-> X*so that the quotient space X* is not Hausdorff.
A4. Let X be a topological space, p : X-> Y and q : Y ->Z surjections. Give Y the quotient topology induced by p. Then Z can be given the quotient topologies induced by q or by q ° p. Show that these topologies are the same.
A5. Consider the function p : R ->{a, b, c} given by:
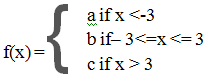
List the open sets in the quotient topology on {a, b, c}.
A6. Let X be a hexagon in the plane with the relative topology from R2 (interior of the hexagon is included). Identify opposite sides of the hexagon with identifcation (arrows) occuring in same direction. What is the resulting space?
Type B problems
B1.Let a surjectivep : X -> X* induce the quotient topology on X*. Give an example
where p is not an open map and one where p is not a closed map (open, closed maps send open sets to open sets or closed sets to closed sets, respectively).
B3. Let D2 be the unit disk {(x1,x2) ∈R2: x11+ x22<=1} with the relative topology fromR2. Define an equivalence relation: x ~ y if x12+x22= y12+y22. Identify the familiar quotient space given by this relation and then show precisely that the quotient topology on this space is the same as the usual one.
B6.Show by induction on g that a genus-g surface with k crosscaps is homeomorphic to the sphere with k + 2g crosscaps.
|
Cases of washington reds in the market
: During the past year, the mean sales of Wshington Reds in cases was 45,000 cases, and the standard deviaiton was 4,450. How many cases of Washington Reds should be brought to market? Assume the sales follow a normal distribution.
|
|
Moral obligations of foreign businesses-respecting culture
: Create arguments supporting position on what moral obligations foreign businesses have regarding changing or respecting local culture in one of these case studies.
|
|
Assembly times and dental expenses
: Find out the z values for 29 and 34 hours. What percent of the garages take between 32 hours and 34 hours to erect? What percent of the garages take between 29 hours and 34 hours to erect?
|
|
Algal bloom kills fish
: A newspaper headline reported Algal Bloom Kills Fish. As you read, you find that the algae did not produce toxins. Describe what actually caused fish death, given that the algae are not toxic?
|
|
What is the resulting space
: Show that these topologies are the same and What is the resulting space and identify the familiar quotient space given by this relation and then show precisely that the quotient topology on this space is the same as the usual one.
|
|
Possibility of expanding the warehouse
: Douglas Boats is considering the possibility of expanding the warehouse for the WM-4 motors. How much should Douglas Boats expand, and how much would it be worth for the company to make the expansion? Assume demand is constant throughout the year.
|
|
What is the resulting ucl value for the line
: From the samples you determine the fraction defective is 0.05 and the standard deviation is 0.01. If the desired confidence level is 99.7 percent, what is the resulting UCL value for the line?
|
|
Evaluate line from one of the romantic poets
: Evaluate the line from one of the Romantic poets to one of Romantic landscape paintings. Explain what you believe the poet and painter is evoking about nature with these works.
|
|
Compute standard deviation of data
: Use information from the modular background readings as well as any good quality resource you can find. Please cite all sources and provide a reference list at the end of your paper.
|