Reference no: EM13893618
Complete the following problems and submit the results both in a Microsoft Word document and EXCEL QM. It is important to clearly show in detail how to get to the answer in both Excel QM and Word documents.
1. Bechtold Construction is in the process of installing power lines to a large housing development. Steve Bechtold wants to minimize the total length of wire used, which will minimize his costs. The housing development is shown as a network. Each house has been numbered, and the distances between houses are given in hundreds of feet.
a. What is the required length of power line required?
b. What is the recommended route for the lines?
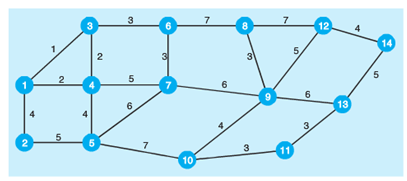
House 7 is currently being demolished and will be removed from the system.
c. With that change, what will be the requirement for power lines and what will the route be?
2. The Rockwell Electronics Corporation retains a service crew to repair machine breakdowns that occur on an average of 3 per day (approximately Poisson in nature). The crew can service an average of 8 machines per day, with a repair time distribution that resembles the exponential distribution.
a. What is the utilization rate of this service system?
b. What is the average downtime for a machine that is broken?
c. How many machines are waiting to be serviced at any given time?
d. What is the probability that more than one machine is in the system?
e. What is the probability that more than two are broken and waiting to be repaired or being serviced?
f. What is the probability that more than three are in the system?
g. What is the probability that more than four are in the system?
3. Juhn and Sons Wholesale Fruit Distributors employ one worker whose job is to load fruit on outgoing company trucks. Trucks arrive at the loading gate at an average of 26 per day, or 3.25 per hour, according to a Poisson distribution. The worker loads them at a rate of 4 per hour, following approximately the exponential distribution in service times.
a. Determine the operating characteristics of this loading gate problem.
b. What is the probability that there will be three or more trucks either being loaded or waiting?
c. Discuss the results of your queuing model computation.
Juhn believes that adding a second fruit loader will substantially improve the firm's efficiency. He estimates that a two-person crew, still acting like a single-server system, at the loading gate wills double the loading rate from 4 trucks per hour to 8 trucks per hour.
d. Analyze the effect on the queue of such a change and compare the results with those found in (a) above.
Truck drivers working for Juhn and Sons are paid a salary of $30 per hour on average. Fruit loaders receive about $18 per hour. Truck drivers waiting in the queue or at the loading gate are drawing a salary but are productively idle and unable to generate revenue during that time.
e. What would be the hourly cost savings to the firm associated with employing two loaders instead of one?
Juhn and Sons are considering building a second platform or gate to speed the process of loading their fruit trucks. This, they think, will be even more efficient than simply hiring another loader to help out the first platform. Assume that workers at each platform will be able to load 4 trucks per hour each and that trucks will continue to arrive at the rate of 3.25 per hour.
f. Find the waiting line's new operating conditions.
g. Is this new approach indeed speedier than the other two already considered?
4. Customers arrive at an automated coffee vending machine at a rate of 3 per minute, following a Poisson distribution. The coffee machine dispenses a cup of coffee in exactly 15 seconds.
a. What is the average number of people waiting in line?
b. What is the average number in the system?
c. How long does the average person wait in line before receiving service?