Reference no: EM132366091

Assignment 1 - Linear Algebra Questions

Q1. a) Define what it means for the vectors v₁, . . . , v_n, in a vector space V over a field K to be linearly independent.

b) Define the rank of a matrix.

In the following questions, justify your answers.

c) Compute the rank of the 4(i) x 6(j) matrix B_4,6 whose (i, j) entry is j:

d) For integers m, n ≥ 1, compute the rank of the m x n matrix A_m,n all of whose entries equal 1.

e) Compute the rank of the 5 x 5 matrix A whose (i, j) entry is 5(i - 1) + j:

For each of the following assertions, if the statement is true, then give a proof, if it is false, then give a counterexample. You can cite results from the lectures without proof, but make sure that it is clear what you are using.

Let V be a vector space over a field K and let v₁, v₂, v₃ and u be vectors in V.

f) If v₁, v₂, v₃ are linearly independent, then v₁, v₂, v₃ + v₁ are linearly independent.

g) If v₁, v₂, v₃, u are linearly independent, then v₁, v₂, v₃ are linearly independent.

h) If v₁, v₂, v₃ are linearly independent, then v₁ + v₂ + v₃ might be 0.

i) If v₁, v₂, v₃ are linearly independent, then v₁ - v₂, v₂ - v₃, v₃ - v₁ are linearly independent.

j) If v₁, v₂, v₃ span V, then v₁, v₂, v₃, u also span V.

k) If v₁ = 0, then v₁, v₂, v₃ cannot span V.

l) If v₁ = 0, then v₁, v₂, v₃ cannot be linearly independent.

Q2. a) Show that the eigenvalues of the matrix

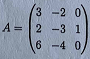
are 1,0, -1, and find the corresponding eigenvectors.

Let V be a vector space over R and let T: V → R³ be a linear transformation. Let v₁, v₂, v₃ ∈ V be three vectors of V and let e₁, e₂, e₃ ∈ R³ be the standard basis vectors. Suppose that

T(v₁) = e₂ - e₃, T(v₂) = -e₁ + e₃, T(v₃) = e₁ - e₂.

b) Show that v₁, v₂ are linearly independent.

c) Find real numbers a₁, a₂, a₃ ∈ R, not all zero, such that a₁v₁ + a₂v₂ + a₃v₃ is in the kernel of T.

d) Suppose also that v₁, v₂, v₃ is a basis of V. Write the matrix of the linear transformation T above with respect to the basis v₁, v₂, v₃ of V and e₁, e₂, e₃ of R³.

Q3. Let n be a positive integer and let A be a square n x n matrix with real entries.

a) Define what are eigenvalues and eigenvectors for the matrix A.

b) Define what it means for the matrix A to be diagonalizable.

Let a, b, c ∈ R be real numbers and let U_a,b,c be the matrix

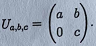
c) Find a choice of a, b, c ∈ R for which the matrix U_a,b,c is invertible. Justify your answer.

d) Find a choice of a, b, c ∈ R for which that the matrix U_a,b,c is diagonalizable and not invertible. Justify your answer.

e) Find a choice of a, b, c ∈ R for which the matrix U_a,b,c is neither diagonalizable nor invertible. Justify your answer.

f) Let C be a 2 x 2 matrix with real entries. Suppose that for every column vector v in R² the two vectors v, Cv are linearly dependent. Show that the matrix C is a multiple of the identity matrix.

Q4. Let A and B be the matrices with real coefficients

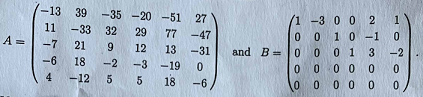
You may use without proof that B is the row reduced form of A.

a) What is the rank of A? Justify your answer.

b) Give a basis for the image of A. Justify your answer.

c) What is the nullity of A? Justify your answer.

d) Give a basis for kernel of A. Justify your answer.

e) Find a row reduced from of the matrix.

Q5. Let R[x]₃ be the real vector space of polynomials of degree at most 3 in the variable x and let T be the function

T : R[x]₃ → R[x]₃

p(x) |→ xp'(x) - p(x).

a) Show that T is a linear transformation.

b) Compute T(1), T(x), T(x²), T(x³).

c) Find the dimension of the image of T.

d) Find a basis for the kernel of T.

e) Does there exist a polynomial of degree 2 not contained in the image of T? Justify your answer.

f) Does there exist a positive integer n such that the rank of Tⁿ is at most 2? Justify your answer.

Assignment 2 - Introduction to Quantitative Economics

Section A: Answer ALL THREE questions.

Q1. Consider a market with inverse demand p = 100 - 2Q. Firms have no fixed cost and constant marginal cost c.

(a) Derive the firms' outputs and profits when this market is served by Cournot duopolists.

(b) How do outputs and profits vary with c?

(c) Suppose the firms also have a fixed cost of F in addition to the marginal cost c. How does F alter the best response functions and Nash equilibrium? Explain in words. (For technical reasons, assume that both firms still produce a positive level of output in equilibrium.)

Q2. Consider two players simultaneously deciding whether to contribute to a public good - the good is said to be public because, if it is made available, an agent who free-rides by paying nothing gets just as much pleasure from its enjoyment as an agent who paid for it. If at least one agent contributes to the construction of the public good, both agents will enjoy a payoff of 4 from the public good. If neither contributes, the good is not constructed and neither player gets enjoyment from the project. If one or both players contribute, then the good is constructed and each player enjoys a payoff of 4 minus the contribution cost 1 if that player has contributed. Assume that the costs are common knowledge to both players.

(a) Fill the payoffs of a, b, c, d, e, f, g, and h in the following table using the information provided above.

		Player 2
		Don't contribute	Contribute
Player 1	Don't contribute	a, b	c, d
	Contribute	e, f	g, h

(b) Find all pure-strategy Nash Equilibrium(s) to the game.

(c) Find the Mixed Strategy Nash Equilibrium.

Q3. The following figure shows the demand curve for Good X in a perfectly competitive market. Later, the government grants one of the firms the exclusive right to manufacture and sell Good X. MR represents the marginal revenue curve of the firm when it operates as a monopoly. The marginal cost of producing Good X is constant at $5.

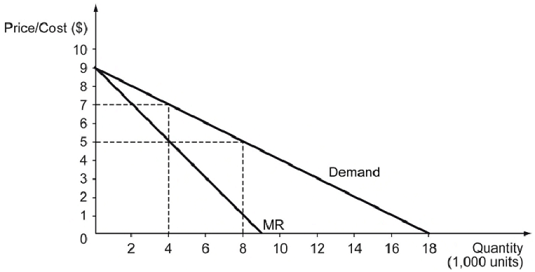
(a) What is the quantity supplied when the market is perfectly competitive? What happens to the quantity supplied once the market changes to a monopoly? Explain your answers in words.

(b) What is the market price when the market is perfectly competitive? What is the market price when the market changes to a monopoly? Explain in words.

(c) Compare the consumer surplus when the market is perfectly competitive and the consumer surplus when the market is a monopoly. Is there any producer surplus or deadweight loss in either case? If yes, then how much?

Section B: Answer ALL THREE questions.

Please use a separate booklet.

Q4. Consider a small open economy which is defined by the following system of equations and identities:

Y = C + I + G + NX

G = G^-, T = T^-

C = C₀ + α(Y - T) (α ∈ (0, 1))

I = I₀ + βr (β < 0)

NX = NX₀ + γε (γ < 0)

(a) Explain analytically AND mathematically, why in this economic system IS equation cannot be defined as it was defined in a closed economy?

(b) Find the difference between national saving and investment if:

Y = 8000, G = 2500, T = 2000

C = 500 + 2/3 (Y - T)

I = 900 - 50r

r = r* = 8

(c) Knowing NX = 1500 - 250ε, what should be the real exchange rate ε to equilibrate the current account with the net capital outflow if we assume the income balance (IB) and the net unilateral transfer (NUT) are zero.

Q5. Two countries A and B are described by the Solow growth model. The information we have about these countries are summarised in the following table:

Country	Production Function	Saving out of Income	Population Growth	Technological Progress	Depreciation Rate
A	F (K, L) = AKαL1-α α ∈ (0, 1)	32%	1% per year	2% per year	5% per year
B	F (K, L) = AKαL1-α α ∈ (0, 1)	10%	3% per year	2% per year	5% per year

(a) What is the per-worker production function f(k)?

(b) Solve for the ratio of country A's steady state income per-worker to country B's.

(c) If the parameter α in the production function takes the conventional value of about 1/3, how much higher should income per worker be in country A compared to country B?

(d) Income per worker in A is 16 times income per worker in B. Can you explain this fact by changing the value of the parameter α? What must it be?

Q6. Suppose that an economy has the Phillips curve π = π_-1 = 0.5(u - 0.05).

(a) What is the natural rate of unemployment?

(b) Graph (fully labelled) the short-run and long-run relationship between inflation and unemployment.

(c) How much cyclical unemployment is necessary to reduce inflation by 4 percentage points? Using Okun's law, compute the sacrifice ratio.

Note - In Assignment 1 LINEAR ALGEBRA: definitions on paper are no need to be answered. Question one is compulsory and expert can choose from question2-5 (pick 3 to answer). In assignment 2 INTRODUCTION TO QUANTITIVE ECONOMICS answer all questions.