Reference no: EM131035228

1. Mean-variance portfolio theory and parameter uncertainty in Markowitz.

(a) Consider N assets indexed by i = 1, ..., N. Let σ_i² denote the variance of the rate of return R_i on asset i and σ_ij denote the covariance between R_i and R_j, for i ≠ j.

i. Write the variance o of an equally-weighted port-folio of the N assets.

ii. Assume all assets have equal volatility σ = 0.2 and all pairs of assets have the same correlation p = 0.25. What does the standard deviation of the portfolio converge to as N goes to infinity?

(b) A portfolio of stocks has expected return μ_s = 8% and standard deviation σ_s = 20%. A portfolio of bonds has expected return μ_B = 7% and standard deviation μ_B = 10%. Let p denote the correlation between the returns on these two portfolios.

i. Draw a graph representing all risk-return profiles that can be obtained in the (σ, μ)-space for p ∈ (0, 1) and for p = 1, assuming there is no constraint on short-selling.

ii. Suppose there is a riskfree asset with rate of return R_f = 5% and p = 0.95. What is the composition of the tangency portfolio?

iii. Consider a mean-variance investor with utility function U(ω) = μ^ε_P - (λ/2)σ²_P, where μ_ε^P = ω'μ^ε and σ²_P = ω'Σω (all notations are standard). Compute the optimal portfolio weights on the two risky assets assuming λ = 5.

iv. Now assume there is a short-sale constraint and no riskfree asset. Characterize the set of all combinations of the bond and stock portfolios which yield an expected rate of return of 6%.

(c) Summarize the analysis in the paper by Kan and Zhou (JFQA, 2007) discussed in the lecture. What assumption do they make on the joint distribution of asset returns? What metric do they use to assess the cost of estimation error? Comment on the impact of estimation error in first and second moments on portfolio performance. Finally, how could one extend their analysis, using simulations to assess the cost of estimation error?

2. Bayesian portfolio choice and shrinkage estimators.

(a) Suppose you have T iid observations on past returns (R₁, R₂, ..., R_T) drawn from N(μ, σ²), where σ² is known but μ is unknown. Let R denote the sample average of the observations. Suppose your prior about μ is N(μ₀, σ₀²).

i. What is the interpretation of σ₀²? What is the interpretation of σ²/σ₀²? What is the interpretation of σ²/(Tσ₀²)?

ii. What is the posterior density for the unknown mean μ? You do not need to prove your result but an interpretation of the formula(s) is required.

iii. Define the concept of predictive distribution and its role in Bayesian portfolio choice. What is the predictive distribution for the rate of return R in the above example? You do not need to prove your result but an interpretation is required.

iv. If μ₀ = R, a Bayesian investor holds the same portfolio as one who uses a plug-in rule with sample moments. Do you agree with this statement?

(b) There are two types of assets. Good quality assets (type-G assets) can have an annual rate of return equal to 4% or 6% with equal probability. Bad quality assets (type-B assets) can earn a rate of return of 4% with probability 3/4 or 0% with probability 1/4. You hold an asset but are completely ignorant about its quality. You learn from a trustworthy source that bad assets account for 1/3 of the total number of assets. A year later, the realized rate of return on your asset is 4%.

i. What is the probability that you own a good asset?

ii. What is the predictive distribution of the return on your asset?

(c) What is the rationale for using a shrinkage estimator of mean returns when dealing with a large number of assets? What is a standard choice for the target? How does the optimal shrinkage intensity (i.e., the weight given to the target) depend on the number of assets N and on the number of past observations T?

3. Black-Litterman

Assume there is a riskfree asset and the market comprises two risky assets A and B, whose standard deviations and correlation are known: σ_A = 10%, σ_B = 20% and p = 0.5. Each asset accounts for half of the market portfolio.

(a) Compute the vector of equilibrium expected excess re-turns μ⁰, assuming the average market risk aversion is λ_A = 2.5.

(b) Your analyst believes asset A will earn 1% in excess of the riskfree rate, while asset B will earn an excess return of 7%. Write down a matrix P and a vector v summarizing these views.

(c) Assume the precision matrix for the prior is Λ^-1 =-(τ)^-1 Σ^-1 where Σ is the covariance matrix of returns on assets A and B and τ = 0.02. Compute Λ^-1. What is the rationale for the small value of τ? How does the value of τ relate to your confidence in CAPM?

(d) Recall that in the Black-Litterman model, the posterior distribution for the unknown vector of excess returns μ^ε is multi-variate normal, with the following mean and covariance matrix:

E(μ^ε|v) = {Λ^-1 + P'Ω^-1P]^-1[Λ-1 μ^ε,0 + P'Ω^-1v],

Var (μ^ε|v) = [Λ^-1 + P'Ω^-1P]^-1.

What does the matrix Ω stand for? Interpret these two formulas.

(e) Assume the errors in the views of your analyst regarding assets A and B are uncorrelated. The precision of the view on asset A is 5,000. The precision of the view on asset B is 1,250. Assume your own coefficient of risk aversion is λ = 2.

i. Apply the Black-Litterman approach to determine the optimal weights on assets A and B. What fraction of wealth do you optimally invest in the riskfree asset?

ii. What fraction of your risky investments do you allocate to asset A? How does it compare to the weight of asset A in the risky portfolio? Interpret your finding.

4. Linear factor models and APT.

(a) Consider a two-factor model of asset returns

Ri = α_i + β_i1f₁ + β_i2f₂ + ε_i

for a large number of securities indexed by i. Assume the factors have zero mean (i.e., E(f_i) = 0) and E(ε_i) = 0. A riskfree bond is available for borrowing and saving at rate R_f = 5%.

i. What is the defining property of a "well-diversified portfolio"?

ii. Assume a well-diversified portfolio A has a beta β_A1 of 1 on factor 1 and a beta β_A2 of 0.5 on factor 2. Another well-diversified portfolio B has a beta β_B1 of 2 on factor 1 and a beta β_B2 of 1.5 on factor 2. Find a portfolio of portfolios A and B that has no exposure to factor 2. What is its exposure to factor 1?

iii. Use your answer to part (ii) to show how to form a well-diversified portfolio with a unit beta on factor 1 and a zero beta on factor 2. What is its expected rate of return as a function of mean returns E(R_A) and E(R_B)?

iv. Suppose the expected excess rates of return on well-diversified mimicking-factor portfolios for factors 1 and 2 are 8% and -2%, respectively. Consider a security with beta 1.5 on factor 1 and 0.2 on factor 2. What does APT imply for the expected return on this security? Justify your answer carefully.

(b) Consider the Carhart four-factor model (Carhart, 1997).

i. What are the factors in this model? How are they constructed?

ii. Explain the use of this model in the context of mutual fund performance evaluation.

(c) How would you estimate country and industry factors based on historical data on international stock returns, using a characteristic-based factor model along the lines of the paper by Heston and Rouwenhorst (1995)?

5. Passive/active asset management and Treynor-Black model.

(a) What is the implication of CAPM for asset management?

(b) Discuss the implications of multi-factor equilibrium asset pricing models for asset management.

(c) Given some reference asset pricing model, what does it mean that a strategy earns "abnormal" returns? In what sense are results on anomalies model-dependent?

(d) How can overreaction explain the value premium?

(e) Define the information ratio of an active manager, given some benchmark index. Why is the information ratio relevant?

(f) Consider three assets 1, 2, and 3 with non-zero alpha against the benchmark. Their alphas and their residual variances are summarized as follows:

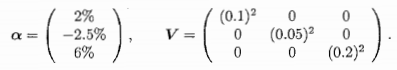
Note that the idiosyncratic components of the three asset returns are assumed to have zero correlation.

i. What is the composition of the optimal active port-folio?

ii. Suppose that instead of investing in the benchmark index and the riskfree rate, you optimally combine the index, the riskfree rate and the optimal active portfolio. How does this affect your (ex-ante) Sharpe ratio?

6. Delegated asset management and performance evaluation.

(a) Consider a sponsor and an investment manager. Two investment opportunities are available to the manager, and she can invest in only one of them. Asset A earns an annual rate of return of 20% or 5% with equal probability. Asset B earns an annual rate of return of 100% or -50% with equal probability. Let W₀ denote the initial amount of managed wealth and W₁ the wealth after one year. Assume the sponsor maximizes his expected utility E[u(W₁)] , where

u(x) = x^{1- γ}/1- γ,  γ > 0.

i. Assume γ = 0.8. What asset would the sponsor pick if he was to choose between assets A and B? Does the value of W₀ matter?

ii. Assume the manager maximizes E[u(C)], where C denotes her compensation. Suppose she has the same risk aversion as the sponsor γ = 0.8 and is remunerated as a fraction π ∈ (0, 1) of terminal wealth W₁. What asset does the manager choose to invest in? Does the value of π matter?

iii. Now assume the manager has risk aversion γ = 0.2 and is remunerated as a fraction of terminal wealth W₁. What asset does she invest in? Comment on your result.

iv. Consider the following compensation scheme: the manager earns 2% of initial wealth W₀ (paid upfront at t = 0) and 20% of the profit she generates (i.e., in case of negative return, the manager only gets the 2% fee). Under that scheme, what asset would the sponsor prefer, assuming that he cares about his final wealth net-of-fees? Assume the manager has risk aversion γ = 0.8. What asset does she choose to invest in? Comment on your result.

(b) Consider four assets A, B, C, D, whose means, variances and covariances are known. Suppose you hire two managers. Manager 1 is restricted to invest in assets A and B, while manager 2 is restricted to invest in assets C and D. There is a riskfree rate R_f and each manager's mandate is to maximize the Sharpe ratio of his/her portfolio. Your own objective is to obtain the highest possible Sharpe ratio by allocating your wealth between the two managers. Describe how funds are allocated. Is this organization of the investment process efficient?

(c) How would you test for market timing ability of a given manager? Assume first you only have data on portfolio returns. What if you also have data on holdings?

(d) Explain the characteristic-based methodology employed by Daniel, Grinblatt, Taman and Wermers (1997) to construct a measure of the stock picking skill of a manager.

(e) Let R_f denote a constant riskfree rate. Consider a linear factor model of asset excess returns:

R_i^e = μ_i^e + _k=1Σ^kβ_ikf_k + ε_i,                  i = 1 , . . . ., N,

where E(f_k) = 0 and E(ε_i) = 0. Let p_k denote the well-diversified mimicking portfolio for factor k and μ_pk^e = E(R_pk^e) denote its expected excess rate of return.

i. Show that one can write R_i^e = α_i+ _k=1Σ^kβ_ikR_pk^e+ ε_i. What is the expression for ai? What is it capturing?

ii. Consider a portfolio q of the N assets with time-varying weights w_it. The rate of return on the portfolio in period t is R_qt = _i=1Σ^N w_itR_it. Let β_qk,t denote the beta of portfolio q on factor k in period t. Show that

E[R_qt^e] = _i=1Σ^NE[w_it] α_i+ _k=1Σ^kcov(β_qk,t,R_pk,t^e) + _k=1Σ^KE[β_qk,t] μ_pk^e.

Interpret this decomposition.

Useful formula: inverse of a two-by-two matrix

Consider a matrix 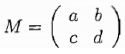with ad -  bc ≠ 0. Then