Reference no: EM131032157

Question 1

A study of students taking Statistics 101 was done. Four hundred students who studied for more than 10 hours averaged a B. Two hundred students who studied for less than 10 hours averaged a C. This difference was significant at the 0.01 level. What does this mean?

A. The probability that the difference was due to chance alone is greater than 0.01.
B. There is less than a 0.01 chance that the first group's grades were better by chance alone.
C. The improvement was due to the fact that more people studied.
D. There is not enough information to make any conclusion.

Question 2

A bag contains four chips of which one is red, one is blue, one is green, and one is yellow. A chip is selected at random from the bag and then replaced in the bag. A second chip is then selected at random. Make a list of the possible outcomes (for example, RB represents the outcome red chip followed by blue chip) and use your list to determine the probability that the two chips selected are the same color. (Hint: There are 16 possible outcomes.)

A. 1/4
B. 3/4
C. 2/16
D. 3/16

Question 3

A sample space consists of 46 separate events that are equally likely. What is the probability of each?

A. 1/24
B. 1/46
C. 1/32
D. 1/18

Question 4

A die with 12 sides is rolled. What is the probability of rolling a number less than 11? Is this the same as rolling a total less than 11 with two six-sided dice? Explain.

A. 2/6
B. 3/6
C. 4/6
D. 5/6

Question 5

Suppose you have an extremely unfair coin: the probability of a head is 1/3 and the probability of a tail is 2/3. If you toss the coin 72 times, how many heads do you expect to see?

A. 12
B. 22
C. 24
D. 26

Question 6

Suppose you have an extremely unfair coin: the probability of a head is 1/5, and the probability of a tail is 4/5. If you toss the coin 40 times, how many heads do you expect to see?

A. 8
B. 6
C. 5
D. 4

Question 7

On a multiple choice test, each question has 6 possible answers. If you make a random guess on the first question, what is the probability that you are correct?

A. 1/5
B. 1/6
C. 1/4
D. 2/5

Question 8

If a person is randomly selected, find the probability that his or her birthday is not in May. Ignore leap years. There are 365 days in a year. Express your answer as a fraction.

A. 335/365
B. 334/365
C. 336/365
D. 30/365

Question 9

The distribution of B.A. degrees conferred by a local college is listed below, by major.
Major Frequency

English 2073
Mathematics 2164
Chemistry 318
Physics 856
Liberal Arts 1358
Business 1676
Engineering 868

9313

What is the probability that a randomly selected degree is not in Business?

A. 0.7800
B. 0.8200
C. 0.8300
D. 0.9200

Question 10

The probability that Luis will pass his statistics test is 0.94. Find the probability that he will fail his statistics test.

A. 0.02
B. 0.05
C. 0.94
D. 0.06

Question 11

Suppose you have an extremely unfair die: The probability of a 6 is 3/8, and the probability of each other number is 1/8. If you toss the die 32 times, how many twos do you expect to see?

A. 2
B. 4
C. 3
D. 5

Question 12

A study of 600 college students taking Statistics 101 revealed that 54 students received the grade of A. Typically 10% of the class gets an A. The difference between this group of students and the expected value is not significant at the 0.05 level. What does this mean in this case?

A. The probability that the difference occurred due to chance is less than 0.05.
B. The probability of getting an A is 10% and only 9% got an A in thisstudy. The difference is less than 5% so it is not significant.
C. There is not enough information to make any conclusion.
D. The probability that the difference occurred due to chance is more than 0.05.

Question 13

A bag contains 4 red marbles, 3 blue marbles, and 7 green marbles. If a marble is randomly selected from the bag, what is the probability that it is blue?

A. 2/11
B. 3/11
C. 5/14
D. 3/14

Question 14

In a poll, respondents were asked whether they had ever been in a car accident. 220 respondents indicated that they had been in a car accident and 370 respondents said that they had not been in a car accident. If one of these respondents is randomly selected, what is the probability of getting someone who has been in a car accident? Round to the nearest thousandth.

A. 0.384
B. 0.380
C. 0.373
D. 0.370

Question 15

A class consists of 50 women and 82 men. If a student is randomly selected, what is the probability that the student is a woman?

A. 32/132
B. 27/66
C. 50/132
D. 82/132

Question 16

If you flip a coin three times, the possible outcomes are HHH, HHT, HTH, HTT, THH, THT, TTH, TTT. What is the probability of getting at least one head?

A. 4/9
B. 5/6
C. 7/8
D. 5/8

Question 17

Suppose you buy 1 ticket for $1 out of a lottery of 1000 tickets where the prize for the one winning ticket is to be $500. What is your expected value?

A. $0.00
B. -$0.40
C. -$1.00
D. -$0.50

Question 18

Sammy and Sally each carry a bag containing a banana, a chocolate bar, and a licorice stick. Simultaneously, they take out a single food item and consume it. The possible pairs of food items that Sally and Sammy consumed are as follows.

chocolate bar - chocolate bar
licorice stick - chocolate bar
banana - banana
chocolate bar - licorice stick
licorice stick - licorice stick
chocolate bar - banana
banana - licorice stick
licorice stick - banana
banana - chocolate bar

Find the probability that no chocolate bar was eaten.

A. 4/9
B. 5/9
C. 7/9
D. 5/8

Question 19

Suppose you pay $1.00 to roll a fair die with the understanding that you will get back $3.00 for rolling a 5 or a 2, nothing otherwise. What is your expected value?

A. $1.00
B. $0.00
C. $3.00
D. -$1.00

Question 20

Joe dealt 20 cards from a standard 52-card deck, and the number of red cards exceeded the number of black cards by 8. He reshuffled the cards and dealt 30 cards. This time, the number of red cards exceeded the number of black cards by 10. Determine which deal is closer to the 50/50 ratio of red/black expected of fairly dealt hands from a fair deck and why.

A. The first series is closer because 1/10 is farther from 1/2 than is 1/8.
B. The series closer to the theoretical 50/50 cannot be determined unless the number of red and black cards for each deal is given.
C. The second series is closer because 20/30 is closer to 1/2 than is 14/20.
D. The first series is closer because the difference between red and black is smaller than the difference in the second series.

Question 21

In a poll0 voters in a certain state, 61% said that they opposed a voter ID bill that might hinder some legitimate voters from voting. The margin of error in the poll was reported as 4 percentage points (with a 95% degree of confidence). Which statement is correct?

A. The reported margin of error is consistent with the sample size.
B. There is not enough information to determine whether the margin of error is consistent with the sample size.
C. The sample size is too small to achieve the stated margin of error.
D. For the given sample size, the margin of error should be smaller than stated.

Question 22

Sample size = 400, sample mean = 44, sample standard deviation = 16. What is the margin of error?

A. 1.4
B. 1.6
C. 2.2
D. 2.6

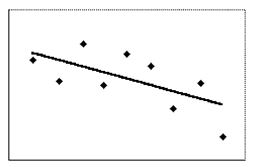
Question 23

Select the best fit line on the scatter diagram below.

 

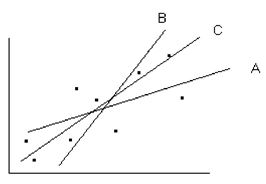
A. A
B. B
C. C
D. None of the lines is the line of best fit

Question 24

Which graph has two groups of data, correlations within each group, but no correlation among all the data?

A.

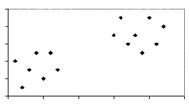
B.

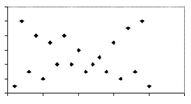
C.

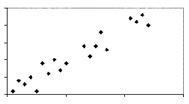
D.

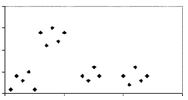
Question 25

Eleven female college students are selected at random and asked their heights. The heights (in inches) are as follows:

67, 59, 64, 69, 65, 65, 66, 64, 62, 64, 62

Estimate the mean height of all female students at this college. Round your answer to the nearest tenth of an inch if necessary.

A. It is not possible to estimate the population mean from this sample data
B. 64.3 inches
C. 64.9 inches
D. 63.7 inches

Question 26

Write possible coordinates for the single outlier such that it would no longer be an outlier.

 

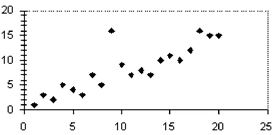
A. (23, 18)
B. (20, 5)
C. (15, 15)
D. (12, 15)

Question 27

The scatter plot and best-fit line show the relation among the data for the price of a stock (y) and employment (x) in arbitrary units. The correlation coefficient is 0.8. Predict the stock price for an employment value of 6.

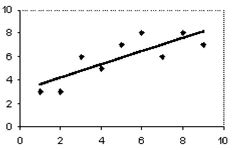
A. 8.8
B. 6.2
C. 8.2
D. None of the values are correct

Question 28

Among a random sample of 150 employees of a particular company, the mean commute distance is 29.6 miles. This mean lies 1.2 standard deviations above the mean of the sampling distribution. If a second sample of 150 employees is selected, what is the probability that for the second sample, the mean commute distance will be less than 29.6 miles?

A. 0.8849
B. 0.5
C. 0.1131
D. 0.1151

Question 29

The scatter plot and best-fit line show the relation among the number of cars waiting by a school (y) and the amount of time after the end of classes (x) in arbitrary units. The correlation coefficient is -0.55. Determine the amount of variation in the number of cars not explained by the variation time after school.

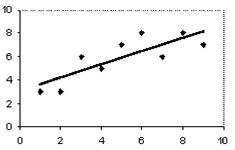
A. 55%
B. 70%
C. 30%
D. 45%

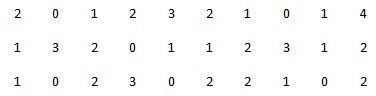
Question 30

A random sample of 30 households was selected from a particular neighborhood. The number of cars for each household is shown below. Estimate the mean number of cars per household for the population of households in this neighborhood. Give the 95% confidence interval.

A. 1.14 to 1.88
B. 1.12 to 1.88
C. 1.12 to 1.98
D. 1.14 to 1.98

Question 31

30% of the fifth grade students in a large school district read below grade level. The distribution of sample proportions of samples of 100 students from this population is normal with a mean of 0.30 and a standard deviation of 0.045. Suppose that you select a sample of 100 fifth grade students from this district and find that the proportion that reads below grade level in the sample is 0.36. What is the probability that a second sample would be selected with a proportion less than 0.36?

A. 0.8932
B. 0.8920
C. 0.9032
D. 0.9048

Question 32

Which point below would be an outlier if it were on the following graph?

A. (25, 20)
B. (5, 12)
C. (7, 5)
D. (5, 3)

Question 33

A sample of nine students is selected from among the students taking a particular exam. The nine students were asked how much time they had spent studying for the exam and the responses (in hours) were as follows:

18, 7, 10, 13, 12, 16, 5, 20, 21

Estimate the mean study time of all students taking the exam. Round your answer to the nearest tenth of an hour if necessary.

A. 13 hours
B. 12.2 hours
C. 13.6 hours
D. It is not possible to estimate the population mean from this sample data

Question 34

Select the best estimate of the correlation coefficient for the data depicted in the scatter diagram.

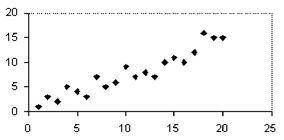
A. -0.9
B. 0.9
C. 0.5
D. -0.5

Question 35

The scatter plot and best-fit line show the relation among the number of cars waiting by a school (y) and the amount of time after the end of classes (x) in arbitrary units. The correlation coefficient is -0.55. Use the line of best fit to predict the number of cars at time 4 after the end of classes.

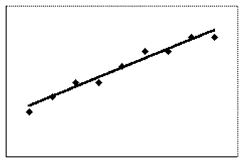
A. 7.0
B. 6.0
C. 8.0
D. 3.5

Question 36

A researcher wishes to estimate the mean amount of money spent per month on food by households in a certain neighborhood. She desires a margin of error of $30. Past studies suggest that a population standard deviation of $248 is reasonable. Estimate the minimum sample size needed to estimate the population mean with the stated accuracy.

A. 274
B. 284
C. 264
D. 272

Question 37

Of the 6796 students in one school district, 1537 cannot read up to grade level. Among a sample of 812 of the students from this school district, 211 cannot read up to grade level. Find the sample proportion of students who cannot read up to grade level.

A. 0.14
B. 0.26
C. 211
D. 0.23

Question 38

Suggest the cause of the correlation among the data.

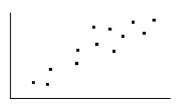
The graph shows strength of coffee (y) and number of scoops used to make 10 cups of coffee (x). Identify the probable cause of the correlation.

A. The variation in the x variable is a direct cause of the variation in the y variable.
B. There is no correlation between the variables.
C. The correlation is due to a common underlying cause.
D. The correlation between the variables is coincidental.

Question 39

A sample of 64 statistics students at a small college had a mean mathematics ACT score of 28 with a standard deviation of 4. Estimate the mean mathematics ACT score for all statistics students at this college. Give the 95% confidence interval.

A. 28.0 to 30.0
B. 25.0 to 27.0
C. 29.0 to 31.0
D. 27.0 to 29.0

Question 40

The graph shows a measure of fitness (y) and miles walked weekly. Identify the probable cause of the correlation.

A. The correlation is coincidental.
B. There is a common underlying cause of the correlation.
C. There is no correlation between the variables.
D. Walking is a direct cause of the fitness.