Reference no: EM132314906

Industrial Statistics Assignment -

Note: All questions are compulsory. Answer in your own words.

1. State whether the following statements are True or False. Give reason in support of your answer:

(a) The process capability of a manufacturing process of a certain type of bolt, with mean diameter 2 inches and standard deviation 0.05 inches, will be 0.30.

(b) If the probability of accepting a lot of satisfactory quality is 0.9401, then the producer's risk will be 0.9401.

(c) Hurwicz criterion is a method to solve the problems that involve decision-making under certainty.

(d) Two independent components of a system are connected in series. If the reliability of these components are 0.8 and 0.6 respectively, then the reliability of the system will be 0.92.

(e) For a two person zero sum game, the payoff matrix is given below:

		Player B
		B1	B2	B3	B4	B5
Player A	A1	3	4	5	-2	3
	A2	1	6	-3	3	7

Then second column will be dominated by the first column.

Q2. (a) A glass manufacturer produces hand mirrors. Each mirror is supposed to meet company standards for such things as glass, color of handle, and so on. To control for these features, the company quality people randomly sample 40 mirrors in every shift and determine how many of the mirrors are out of compliance on at least one feature. Shown here are the data for 15 such samples.

Sample	Number out of Compliance	Sample	Number out of Compliance
1	2	6	0
2	0	7	4
3	6	8	3
4	3	9	2
5	1	10	2

Use the data to construct a suitable chart. Observe the results and comment on the control of the process as indicated by the chart.

(b) A process of manufacturing an item is in statistical control with X⁼ = 250 and R^- = 3.5. The specification limits of the process are 200 ± 81.90. Calculate the process capability. Does it appear that the manufacturing process is capable of meeting the specification requirements? (d₂ = 2.059)

Q3. A leather bag manufacturing company supplies bags in lots of size 150 to a buyer. A single sampling plan with n = 10 and c = 1 is being used for the lot inspection. The company and the buyer decide that AQL = 0.08 and LTDD = 0.16. If there are 15 defective bags in each lit, compute the

i) Probability of accepting the lot,

ii) Producer's risk and consumer's risk,

iii) AOQ, if the rejected lots are screened and all defective bags are replaced by non-defectives, and

iv) Average total inspection.

Q4. An office supply company ordered a lot of 4,000 pens. When the lot arrives the company inspector will randomly inspect 15 pens. If more than three pens in the sample are non-conforming, the lot will be rejected. If fewer than two pens are non-conforming, the lot will be accepted. If two, three pens are non-conforming, a second sample of size 10 will be taken. The value of c₂ is 3. Suppose the inspector finds two nonconforming items in the first sample and two in the second sample. Also AQL and LTPD are 0.05 and 0.10 respectively. Let incoming quality be 4%.

i) What type of acceptance plan is used here?

ii) What is the probability of accepting the lot at the first sample?

iii) What is the probability of accepting the lot at the second sample?

Q5. The manager of a Flower Shop promises its customers delivery within four hours on all flower orders. All flowers are purchased on the previous day and delivered to Parker by 8.00 AM the next morning. The daily demand for roses is as follows:

Dozens of roses	150	160	170	200
Probability	0.2	0.3	0.4	0.1

The manager purchases roses Rs 50 per dozen and sells them for Rs 150. All unsold roses are donated to a local hospital. How many dozens of roses should Parker order each evening to maximize its profits? What is the optimum expected profit?

Q6. In a small town, there are only two stores, ABC and XYZ that handle sundry goods. The total number of customers is equally divided between the two, because price and quality of goods sold are equal. Both stores have good reputation in the community, and they render quality good customer run annual pre-New Year sales during the first week of January. Sales are advertised through a local newspaper, radio and television media. With the aid of an advertising firm store ABC constructed the game matrix given below. (Figures in the matrix represent a gain or loss of customers).

	Strategy of XYZ
Strategy of ABC	Newspaper	Radio	Television
Newspaper	30	40	-80
Radio	0	15	-20
Television	90	20	50

Determine optimal strategies for both ABC and XYZ.

Q7. (a) The system shown below is made up of ten components. Components 2, 3 and 4 are not identical and at least two component of this group must be available for system success.

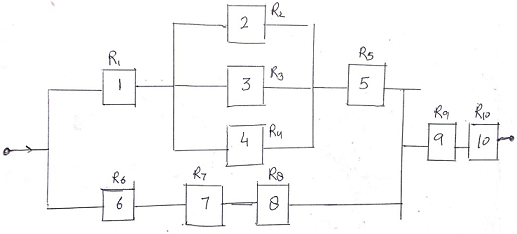
What is the system reliability if R₁ = R₅ = 0.85, R₆ = R₇ = R₈ = 0.80, R₉ = R₁₀ = 0.70, R₂ = 0.40, R₃ = 0.50 and R₄ = 0.60.

(b) A system having Weibull failure distribution with pdf as

f(t) = (1/θ)e^-t/θ t ≥ 0

i) Compute the reliability function of the system,

ii) Find the reliability for a 100 days mission for θ = 2,

iii) Show that the hazard rate is constant,

iv) Find the MTTF, and

v) What is the life of the system if reliability of 0.90 is desired?

Q8. A factory producing dry-cells wanted to test the life of cells produced daily. The cells will be considered satisfactory if their life is 25 hours. For this, a sample of 4 cells was drawn on 7 consecutive days. The results are as follows:

Day 1	Day 2	Day 3	Day 4	Day 5	Day 6	Day 7
24	16	20	26	20	25	26
20	23	25	18	22	23	24
25	23	24	28	24	25	20
20	20	21	20	22	20	25

i) Estimate the process mean.

ii) Determine the centre line and control limits of the control charts for controlling the process mean and process variability.

iii) Plot the charts on the graph papers.

iv) What managerial decisions should be made on the basis of these charts?

v) If necessary, compute revised control limits.