Reference no: EM13274050

1. An object on a horizontal spring oscillates with a period of 1.20 s and an amplitude of 10.0 cm. At t = 0 s, the object is 5.00 cm to the left of equilibrium and is moving to the left.

a) What is the phase constant of the motion?

b) What are its position and direction of travel at t = 2.00 s?

c) What is the first time when the object is at maximum velocity?

2. A shaker table is a tool used in engineering tests to find out how a device responds to vibrations. It is simply a platform that is able to oscillate vertically or horizontally with adjustable amplitude and frequency. Suppose a device of mass, m, is placed on top of the shaker table but not secured to it (it is placed loose on the table). The table is now set oscillating vertically in simple harmonic motion with an amplitude of 1 cm.

a) What is the maximum acceleration of the table without the device leaving contact with it?

b) At what frequency of oscillation does the device first start to leave contact with the table? At what point in the table's motion does the device leave contact with the table at this frequency?

What is the period and angular frequency of the table at this frequency?

c) At the frequency found in b) what is the maximum speed of the table? At what point in the table's motion does it move at this speed?

d) Now suppose the table is set to oscillate horizontally (no vertical oscillation) at a frequency of 10 Hz. It is found that when the oscillation amplitude is 0.500 mm the device begins to slip on the surface of the table. What is the coefficient of static friction between the shaker table surface and the device?

3. A 500 g mass hangs at the end of a 40 cm long string. It is struck by a 250 g mass moving at 0.5 m/s to the right. They undergo an elastic collision.

a) Find the velocities of both masses immediately after the collision.

b) Find the maximum height to which the pendulum rises

c) There are two ways to find the angular frequency ω: one from the pendulum equation, and one from the vmax equation. Use both and compare your answers

4. The graph at right shows the motion for a mass on a spring.

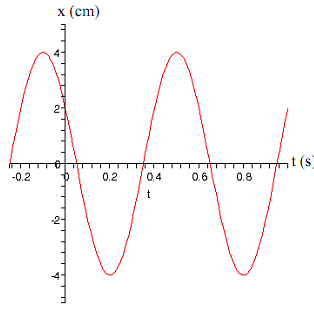
a) What are the amplitude, frequency, period and angular frequency of the mass's motion?

b) What is the phase constant of the oscillation?

c) Write the position as a function of time, x(t).

d) What is the maximum speed of the mass?

e) Suppose the mass is 0.5 kg. What is the spring constant of the spring?

f) What is the total energy of this mass and spring system?