Reference no: EM13729747

1. Consider a voting model with 4 voters: A, B, C and D. The policy space has 2 dimensions, x and y. The voters' ideal points are (x_A,y_A) = (1,1), (x_B,y_B) = (1,3), (x_C,y_C) = (3,3) and (x_D,y_D) = (3,1).

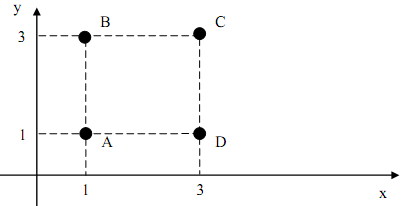
The voters vote sincerely. Assume that their preferences are given by the distance between their ideal point and the implemented policy (x,y). That is, their indifference curves are circles. If a voter is indifferent between 2 candidates, he votes for each with prob. 1/2.

There are 2 candidates, 1 and 2, who compete by simultaneously choosing their platforms, (x1,y1) and (x2,y2). Their objective is to get elected. The candidate who gets the majority of votes wins the elections. If the candidates get the same number of votes, each gets elected with prob. 1/2.

What is the Nash equilibrium of this game?

2. Consider a universalism model of legislatures. There are N districts, N > 1. Each district elects a representative to a legislature. The legislature has to determine spending levels (g1, g2,...,gN) in these districts. The tax burden is shared equally: each district i pays a tax Ti = (g1+ g2+...+gN)/N. The utility of legislator i is ui = a*log(gi) - Ti.

Legislators use a universalism rule. That is, each legislator i picks the desired level of spending gi * in his district, while treating all other legislators' choices as given. Then the legislature passes a bill (g1 *, g2 *,..., gN * ).

a. What is the equilibrium spending level (g1*, g2*,..., gN*)?

b. What are the socially optimal spending levels (g1^o, g2^o,..., gN^o)? How dothey compare to the equilibrium spending levels?

c. Explain why the universalism approach may not be convincing.

3. Suppose that there are 3 legislators: A, B and C. They decide how to split a budget of size 1. Their discount factors are dA = 1, dB = 0.8, dC = 0.7. The rules of the game are as follows.

Stage 1. One legislator is picked randomly to propose a division of the budget. The probabilities with which the legislators are picked are respectively pA = 0.5, pB = 0.3 and pC = 0.2. If the division is approved, each gets his proposed share and the game ends. If the division is not approved, the game moves on to stage 2.

Stage 2. Again, one legislator is picked randomly to make a proposal. The probabilities are the same as above. If the division is approved, each gets his proposed share and the game ends. If the proposal is not approved, the game moves on to stage 3.

Stage 3. Just as before, one legislator is picked randomly to make a proposal. The probabilities are the same as above. If the division is approved, each gets his proposed share and the game ends. If the division is not approved, all legislators get a payoff of 0.

First, suppose that the proposal has to be approved unanimously (by all three legislators).

a. In stage 3, what share would each legislator require to accept somebody else's proposal? What division would each legislator propose if he gets picked? What is the expected payoff of each legislator?

b. In stage 2, what share would each legislator require to accept somebody else's proposal? What division would each legislator propose if he gets picked? What is the expected payoff of each legislator?

c. In stage 1, what share would each legislator require to accept somebody else's proposal? What division would each legislator propose if he gets picked? What is the expected payoff of each legislator?

Now suppose that the proposal only needs a majority vote to pass (i.e. only 1 other legislator must approve it).

d. In stage 3, what share would each legislator require to accept somebody else's proposal? What division would each legislator propose if he gets picked? What is the expected payoff of each legislator?

e. In stage 2, what share would each legislator require to accept somebody else's proposal? What division would each legislator propose if he gets picked? What is the expected payoff of each legislator?

f. In stage 1, what share would each legislator require to accept somebody else's proposal? What division would each legislator propose if he gets picked? What is the expected payoff of each legislator?

4. a. Explain what a retrospective voting rule is.

b. How does retrospective voting affect the politician's behavior and the voter's payoff in dynamic models of elections?

c. When would the disciplining role of retrospective voting unravel?