Reference no: EM131106548

Part 1:

Open a web browser, and navigate to the following web page:

https://serc.carleton.edu/student_videos/index.html#waves

Look for the video called "Standing Waves." Click the DMV player link and start the video. You should see a frame like Figure 1 below:

Using the video controls, you can advance the video one frame at a time. The red LED display on screen indicates the frequency of the motor used to oscillate the string (you can see the motor attached to the right end of the string). The tension in the string is caused by the 50-gram mass hanging from the left end.

As the video plays, the motor frequency is steadily increased. You will see several harmonic modes appear (standing waves consisting of loops on the string). Play the entire video completely before you begin, then reset before you answer the following questions.

1. If there is a 50-gram mass hanging in equilibrium on one end of the string, calculate the tension in the string in Newtons:

2. Click the Horizontal Ruler button, and carefully position the ruler (click and drag) until the 0 cm mark lines up with the left edge of the horizontal portion of string, as shown below in Fig. 2.

3. What is the length of the string (to the nearest cm)? Measure to the center of the vertical shaft of the motor on the right side.

4. Play the video, and pause the video when you see the first harmonic mode appear (one loop). Use the singleframe forward and reverse buttons to make sure that you find the frame with the highest-amplitude loop. What is the frequency corresponding to this loop (the fundamental frequency of the string):

5. What is the wavelength corresponding to the fundamental frequency?

6. What is the speed of the waves on the string? (Use wavelength and frequency to calculate.)

7. If the tension in the string remains the same, and if the string's mass density remains the same, what will be the speed of the waves when you see the second harmonic mode appear (two loops)?

8. If the string is divided into two loops, what will be the wavelength corresponding to the second harmonic mode?

9. Calculate the second harmonic frequency using speed and wavelength:

10. Now play the video until you see two loops appear. Pause the video, and use the single-frame forward and reverse buttons until you find the frame with the highest-amplitude loops. Record the frequency displayed on screen:

11. The on-screen frequency should be close to your calculated frequency. How close? Calculate the percent difference between the two numbers (the difference divided by average . . . refer to previous assignments for examples):

* Do not turn in this assignment until your percent difference is less than 10% . . .

If it is greater than 10%, you need to check your calculations, or perhaps your on-screen data.

12. Now calculate the third and fourth harmonic frequencies, along with the corresponding wavelengths:

13. Do you third and fourth harmonic frequencies match the on-screen frequencies, within a 10% difference?

(They should.) Show your percent difference calculations.

14. Use your calculated speed of the waves on the screen, and the tension in the string, to calculate the linear mass density (μ ) of the string (in kilograms per meter):

15. If you double the tension in the string, but keep the mass density and length the same, what will be the new fundamental frequency? (Show all of your steps below.)

16. On the video, use the pull-down menu at the bottom of the screen to select the 100-gram mass on the end of the string. Play the video, and determine the new fundamental frequency for the string:

17. Calculate the percent difference between the on-screen and calculated values for new f1. Is the percent difference less than 10%?

18. If the percent difference is higher than expected, first check your calculations, then your on-screen observations. If those seem OK, then the reason for the difference may be a change in the string's linear mass density. (In other words, by adding tension to the elastic string, we inadvertently changed μ, as well.) 

The string is elastic, which means that it will stretch when more tension is applied. If the string stretches, its linear mass density will change.

If the string stretches, will its linear mass density increase or decrease? Explain your answer.

Part 2:

Homework Assignment: Energy Conservation in a Cart-Spring System

You may print this sheet and write your answers on it, or write your answers on separate pages (be sure to clearly label each question & answer.)

Open a web browser, and navigate to the following web page:

https://serc.carleton.edu/student_videos/index.html#energy

Look for the video called "Conservation of energy in a cart launched by a spring." Click the DMV link and
start the video. You should see a frame like Figure 1 below:

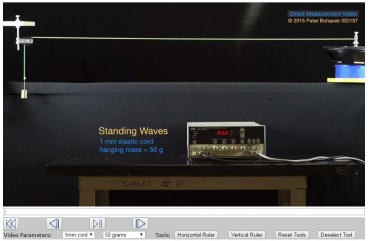
Figure 1: Screenshot using DMV player

Play the video through at least once in its entirety to see the "big picture" first. Then, using the video controls, you can advance the video one frame at a time. Note the scales marked on the screen for measuring position. Using the data available on-screen, answer the following questions. Where calculations are necessary, show ALL of your steps on this page or separate pages. When counting frames, round to the nearest frame (e.g. 2.5 frames would be rounded up to 3 frames). We will be working with many approximations.

- Our system in this exercise will be the cart, the spring, and the Earth. We will measure gravitational energy from the track surface.

- Always include appropriate UNITS when you finish a calculation.

1. What is the frame rate for the video? (You need to play the whole video to see this information.)

2. Before the cart is released, what is the maximum amount the spring is stretched? (Answer in meters, to the nearest 0.01 m.)

3. Before the cart is released, how much elastic energy is stored in the spring? (Include units.)

4. Before the cart is released, what is the system's kinetic energy? 

5. Before the cart is released, what is the system's total mechanical energy?

6. After the cart is released, advance the video frame-by-frame until you notice the string going slack. (In other words, there is no longer a tension force pulling the cart forward.) Notice that "Einstein" is holding his left arm up. Use his arm to track the motion of the cart. More specifically, use the yellow dot he holds in his hand.

How many seconds does it take for the cart to coast forward from 0 cm to 20 cm? (Hint: First count the number of frames, then convert to seconds.)

7. Calculate the average speed of the cart as it coasts from 0 cm to 20 cm. Answer in meters per second.

8. Calculate the kinetic energy of the system as the cart coasts from 0 cm to 20 cm.

9. When the string goes slack, as the cart coasts forward, how much elastic energy remains in the system?

10. Does the gravitational energy of the system change as the cart moves along? Justify your answer.

11. Calculate the total mechanical energy in the system when the string goes slack:

12. Find the percent difference between (a.) the total mechanical energy of the system before cart is released and (b.) the total mechanical energy of the system when the spring goes slack:

13. Let's say that, if the percent difference between two numbers is less than 5%, those two numbers are reasonably close together (close to being the same value). Was the total mechanical energy of the system before the cart's release reasonably close to the total mechanical energy when string went slack?

14. If you answered "No" to the question above, explain what may have happened to the "missing" energy. If you answered "Yes," explain where all of the cart's kinetic energy came from after release.