What is the density matrix for the system

Reference no: EM131290822

Problem 1:

(a) A system is known to be in one of three states. Its probability of being in the first is 1/2 and of being in the second is 1/3. What is the density matrix for the system?

(b) Which, if any, of the following density matrices describe pure states?

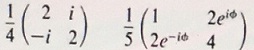
Problem 2: The state of a certain system is described by the density matrix

(a) x ? , y = ?

(b) Verify whether or not the system is in a pure state.

Problem 3

(a) A system is known to be in one of two states. Show that the most general possible density matrix has the form

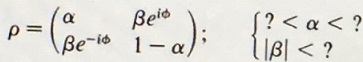
(b) Show that β = ±√(α(1 - α) if the system is in a pure state.

(d) Find α and β (in a representation in which σ_z is diagonal) for a partially polarized beam of particles such that spin parallel to the z-axis occurs twice as often as spin anti-parallel to the z-axis.

Problem 4 The state of polarization of a beam of spin one-half particles is described by the polarization vector P defined in terms of the density matrix p as follows:

P = (σ) =Tr (ρσ).

Supposing P to be determined experimentally, show that

ρ = 1/2 (1 + P.σ).

Reference no: EM131290822

Questions Cloud

Write a brief summary on commentaries : Provide a critical analysis of the author's position. Please note that to be critical does not always mean to be negative. It might be the case that you agree with the author's main arguments. In either case, you need to support your assessment by..

Ethical implications of organizations monitoring : What kind of information is it ethical to collect or unethical to collect? Why? Should managers and organizations inform subordinates they are collecting such information?

Determine the firm''s cash flows on the loan : Determine the firm's cash flows on the loan if LIBOR turns out to be 11.35 percent on April 16, 10.2 percent on July 15, and 8.86 percent on October 14. If you have a financial calculator or spreadsheet, determine the internal rate of return and a..

Find how much the bank should receive for selling this call : The risk-free rate for 45 days is 11.28 percent. All rates are continuously compounded. Use the Black model to determine how much the bank should receive for selling this call for every $1 million of notional principal.

What is the density matrix for the system : A system is known to be in one of three states. Its probability of being in the first is 1/2 and of being in the second is 1/3. What is the density matrix for the system?

Perfume and the scent permeates from computer : Future Innovation Example: Computers that offer smells - click on the perfume and the scent permeates from your computer. You no longer need to go to the store to see if you like it.

Employment relationship from union member rights : Describe the benefits have nonunion employees have gained in their employment relationship from union member rights?

Did luxury tax yield the equity outcome initially expected : Also show a 50% drop i boat sales, after the imposition of the luxury tax. Did the luxury tax yield the equity outcome initially expected? Why?

Should the company lease the equipments : The companies marginal tax rate is 33%. If the before tax borrowing rate for the company is 12%.

User Account

All Pages