Reference no: EM132991232
Question 1: use of a software is not recom-mended
Let X = [X1, X2]T ~ N2(μ, Σ) be a bivariate normal vector, where μ = [μ1, μ2]T and Σ =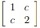 
Let Σ be positive definite and
d2(X, μ) = (X - μ)T Σ-1(X - μ).
(a) Obtain the distribution of Σ-1/2 (X - μ). Show your working.
(b) Let ([X11, X12]T , [X21, X22]T,.....[Xn1, Xn2]T be n independent copies of X and X- = [X~1, X~2]T be the vector of averages
X-1 = Σni=1 Xi1 and X-2 = Σni=1 Xi2
Let F(x) be the cumulative distribution function (CDF) of nd2(X-, μ). Identify F(x) including its parameter(s). Give your reasoning.
(c) Let the significance level α = 0.1 and F(4.61) = 1-α, where F(x) is defined in (b). Suppose that Σ is known. The sample of size n = 4 is randomly sampled from the distribution of X and the sample mean vector x- = [0.3, 0]T. Let Ho: μ = [0, 0]T and H1: μ ≠ [0,0]T. Determine the interval for all c for which the hypothesis Ho will not be rejected at the significance level α = 0.1
(d) Now suppose that E is unknown. What is the distribution of nd2(X-, μ)?
(e) In this framework, what is the decision rule for rejecting the null hypothesis Ho: μ = [0, 0]T.
Question 2: use of a software is not recommended
The multivariate observations of 4 variables were obtained for 20 subjects and these observations were denoted by x1 ..... x20, where each xi is a 4 x 1 vector containing 4 values from the 4 variables. Let the population mean vector be μ = (μ1, μ2, μ3, μ4)T. Suppose we wish to test the following hypotheses involving different contrasts:
H0: μ1 - (μ2+μ3+μ4)/3 = 0, μ2 - (μ1+μ3+μ4)/3 = 0,
μ3 - (μ1+μ2+μ4)/3 = 0, μ4 - (μ1+μ2+μ3)/3 = 0,
Let the significance level for the test be α = 5%.
(a) Explain how to test this hypothesis. In your answer you must include: (i) assumptions made, (ii) test statistic! and (iii) how to decide on rejecting or retaining the null hypothesis.
(b) Write down the T2 simultaneous confidence intervals for all contrasts.
(c) Write down the Bonferroni simultaneous confidence intervals for all contrasts.