What is the cost of the shortest path

Assignment Help Operation Research

Reference no: EM132514222

Question: The following chart was used to compute Dijkstra's algorithm for some network, where we'll interpret the values on each edge as that edge's cost.

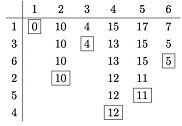
(a) What is the cost of the shortest path from Node 1 to Node 5?

(b) What path do I take to attain the minimum cost from Node 1 to Node 5?

(d) What path do I take to attain the minimum cost from Node 1 to Node 5?

(e) Copy the grid below and fill in as many of the costs as you can from the information in the table above. If you have enough information, put the cost of the (i, j) edge in the cell in row i, column j. Write NEI for "not enough information", and co if i is not connected to j. NOTE: we want the costs of the edges themselves, not the cost of the shortest paths. I have filled in the diagonal values and all values under the diagonal.

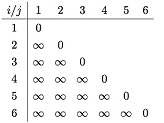
(f) Is it possible to infer from the table the cost of the shortest route from Node 3 to Node 5? If so what is the corresponding route, and why do you know it? If not, can you provide an upper bound for the cost (and provide your reasoning).

Reference no: EM132514222

Questions Cloud

Discuss the various factors contributing to victim movement : 2. Discuss the various factors contributing to the victim movement. Limit your discussion to one or two lines per factor.

Describe how historical problems were managed : Describe how historical problems were managed in the evolution of the U.S. Constitution. Correlate the role of each branch of government with Bill of Rights.

Ransomware-malware and business security : Need a document on " Ransomware, malware, business security" with APA format including sources & bibliography.

Calculate Towing Companys budgeted cash collections : On average, 32% of the sales on account are collected in the month of sale, Calculate Towing Company's budgeted cash collections for September

What is the cost of the shortest path : What is the cost of the shortest path from Node 1 to Node 5 and What is the cost of the shortest path from Node 1 to Node 4

Health issue topic that is relevant to the forces : Locate a current article that examines a health issue topic that is relevant to the forces affecting the delivery of health care such as political

Take note of one form of folklore : While watching, take note of one form of folklore. This can be something very minor, such as a particular gesture or a traditional joke. Or it can be something

How does geographic profiling assist in such cases : Imagine that you are a Federal Bureau of Investigation (FBI) investigator, and you are speaking to new recruits at the FBI training facility in Quantico.

Research example of cyber terrorism : Using the Web or other resources, research an example of Cyber Terrorism. Write a brief Discussion describing the terrorism attack and it's aftermath.

User Account

All Pages