Reference no: EM132012670
Vibration Analysis Questions -
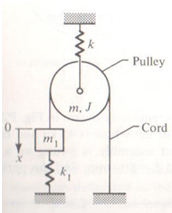
Q1. Use the energy method to determine the equations of motion and the natural frequency for the given system. Assume there is no slippage between the pulley and the cord.
Q2. A helicopter blade and rotor assembly is shown in Fig. Make the necessary assumptions to simplify the problem and deduce the equation of motion for the flapping motion of the blade.

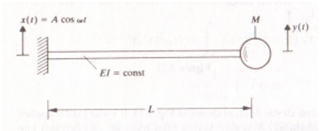
Q3. The left end of the cantilever beam shown in Fig. undergoes the harmonic motion x(t)=A cos(wt). Derive the differential equation for the motion of the mass M and determine the resonance frequency. Assume that the beam is massless and that its bending stiffness EI is constant.
Q4. The support of the viscously damped pendulum shown in Fig. undergoes harmonic oscillation. Derive the differential equation of motion of the system, then assume small amplitudes and solve for θ (t).

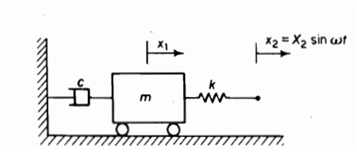
Q5. For the system shown in Fig., set up the equations of motion and solve for the steady state amplitude and phase angle by the use of complex algebra.
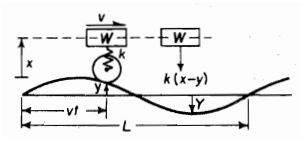
Q6. Fig. represents a simplified diagram of a spring supported vehicle travelling over a rough road. Determine the equation for the amplitude of W as a function of the speed and determine the most unfavorable speed.
Q7. An undamped vibration pickup having a natural frequency of 1 cps is used to measure a harmonic vibration of 4 cps. If the amplitude indicated by the pickup (relative amplitude between pickup mass and frame) is 0.052cm, what is the correct amplitude?
Q8. An aircraft radio weighing 106.75 N is to be isolated from engine vibrations ranging from 1600 to 2200 cpm. What statical deflection must the isolators have for 85 per cent isolation?