Reference no: EM13492805
1. There is a contractual requirement to demonstrate with 90% confidence that a vehicle can achieve a 100-km mission with a reliability of 99%. The acceptance test is performed by running 10 vehicles over a 50,000-km test track.
(a). What is the contractual MTTF? Assuming an exponential distribution:
(b). What is the maximum number of failures that can be experienced on the demonstration test without violating the contractual requirement? (Note: Assume an exponential distribution.)
2. The failure rate for a high-speed fan is given by Mt) = (2 x 104 + 3 x 10-60 / hr, Where t is in hours of operation. The required design-life reliability is 0.95.
(a) How many hours of operation should the design life be?
(b) If, by preventive maintenance, the wear contribution to the failure rate can be eliminated, to how many hours can the design life be extended?
(c) By placing the fan in a controlled environment, we can reduce the contribution of random failure to Mt) by a factor of two. Then, without preventive maintenance, to how many hours may the design life be extended?
(d) What is the extended design life with both preventive maintenance and controlled environment?
3. The following table gives a series of times to repair (man-hours) obtained for a diesel engine.
|
11.6
|
7.9
|
27.7
|
17.8
|
8.9
|
22.5
|
|
3.3
|
33.3
|
75.3
|
9.4
|
28.5
|
5.4
|
|
10.3
|
1.1
|
7.8
|
41.9
|
13.3
|
5.3
|
(a) Estimate the MTTR.
(b) Estimate the repair rate and its 90% confidence interval assuming that the data is exponentially distributed.
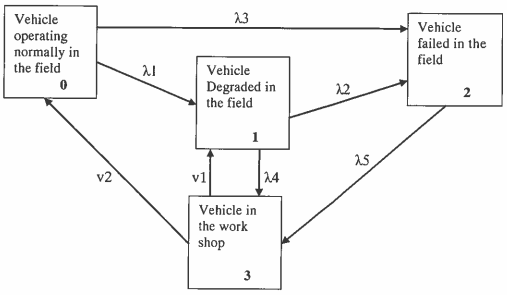
4. Set up the associated Markov differential equations for the following system.
λ3= Failure rate from State-0 to State-2
λ4= Failure rate from State-I to State-3
λ5= Failure rate from State-2 to State-3
v1= Repair rate from State-3 to State-I
v2= Repair rate from State-3 to State-0