Reference no: EM131006216

Question 1. Cache Mapping and Access

Consider a 1 MB cache with 16-word cachelines. Each word is 4-Bytes. This cache uses write-back scheme, and the address is 32 bits wide.

A. Direct-Mapped Cache Fields

Assume the cache is direct-mapped. Fill in the table below to specify the size of each address field of the cache.

Field                      Size (bits)

Cacheline             Offset

Cacheline             Index

Tag

B. Fully-Associative Cache Fields

Assume the cache is fully-associative. Fill in the table below to specify the size of each address field of the cache.

Field                      Size (bits)

Cacheline             Offset

Cacheline             Index

Tag

C. 16-Way Set-Associative Cache Fields

Assume the cache is 16-way set-associative. Fill in the table below to specify the size of each address field.

Field                      Size (bits)

Cacheline             Offset

Cacheline             Index

Tag

Question 2. Average Memory Access Time

Assume the following processor configuration: a dedicated L1 cache for instructions (IL1) and a L1 cache for data (DL1), a shared L2 cache that serves as an intermediate level between each of the L1 caches and the main memory. The figure below shows the hierarchy:

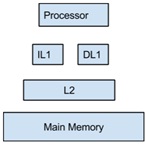
Figure 1: Cache Hierarchy

Processor Spec	Computer A
Cycle Time	1ns
Hit Time to L1(I-L1 or D-L1) and return the data to the processor	1 cycle
1L1 miss rate	8%
DL1 miss rate	15%
Hit Time to L2 and return the data to the L1(I-L1  or D-L1)	6 cycles
L2 miss rate	30%
Main Memory Access Time from L2	50 cycles

Figure 2: Table containing the processor cache Specifications

Out of the total instructions executed in this processor, assume load/store instructions comprise of 25% of the total instructions. Answer the following questions.

A. Calculate AMAT

What is the average memory access time?

B. Processor with no caches

Assume CPI = 1 if the processor has no memory stalls. Without the caches, each memory access would take 52 cycles. What is the CPI of the processor without any caches?

C. Processor with two levels of caches (as in Figure 1)

Assume CPI = 1 if the processor has no memory stalls. What is the CPI of processor with the all the caches? Remember that it takes 50 cycles to access memory from L2.

Question 3. Two-Cycle Instruction Cache

In this problem, we will be examining the performance of the instruction cache on the MIPS assembly program shown on the next page. The first column shows the instruction address for each instruction. Note that these addresses are byte addresses. The value of r1 is initially 64, meaning that there are 64 iterations in the loop. In this problem, we will be considering the execution of this loop with a direct-mapped instruction cache microarchitecture with eight cache lines, and each cacheline is 16B. This means each cache line can hold four instructions and the bottom four bits of an instruction address are the block offset. Hint: The first instruction in the code segment (i.e., addiu r1, r1, -1), is in the middle of a cache line with starting address 0x100.

For this problem, the instruction cache hit time is two cycles, but it is fully pipelined. Tag check occurs in the first cycle, and if it is a hit, the instruction is read in the second cycle. Essentially, this creates a six-stage pipelined processor with the following stages: instruction cache tag check (F0), instruction cache data access (F1), decode (D), execute (X), memory (M), and write-back (W). This also implies the data cache hit time is one cycle.

Assume that jumps are resolved in the decode stage and that branches are re- solved in the execute stage. Assume the miss penalty is three cycles so on a cache miss the pipeline will stay in F0 for a total of three cycles, go into F1 for one cycle, and then continue as normal. You should assume that in every other way, the processor pipeline follows the classic fully-bypassed five-stage pipeline. Assume that the processor does not include a branch delay slot. Assume the processor speculatively predicts all jumps and branches are not taken.

A. Control Hazards

Draw a pipeline diagram illustrating the first iteration of the loop assuming there are no instruction cache misses. Remember that there are two fetch stages (F0 and F1). Show stalls by simply repeating the pipeline stage character (e.g., D) for multiple consecutive cycles.

Use a dash (-) to indicate pipeline bubbles caused by killing instructions (pipeline flushes). You should show all instructions in the first iteration of the loop and the first instruction of the second iteration that you can properly draw the control dependency for the backwards branch.

Address	Instruction	Q3.B Iteration 1 ICache Miss Type	Q3.C Iteration 2 ICache Miss Type
	loop:
0x108	addiu r1, r1,  -1
0x10c	j foo
0x110	addiu r2, r2,  1
0x114	addiu r3, r3,  1
0x118	addiu r4, r4,  1
0x11c	addiu r5, r5,  1
	...
	foo:
0x218	bgtz r1, loop
0x21c	addiu r6, r6,  1
0x220	addiu r7, r7,  1
0x224	addiu r8, r8,  1
0x228	addiu r9, r9,  1

B. First Iteration of the Loop

Fill in the table above. In the appropriate column, write compulsory, conflict, or capacity next to each instruction which misses in the instruction cache to indicate the type of instruction cache misses that occur in the first iteration of the loop. Assume that the instruction cache is initially completely empty. Now draw a pipeline diagram illustrating the first iteration of the loop including instruction cache misses. Clearly indicate the number of cycles it takes to execute the first iteration.

C. Second Iteration of the Loop and overall CPI

Continue to fill in the table above. Write compulsory, conflict, or capacity next to each instruction which misses in the instruction cache to indicate the type of instruction caches misses that occur in the second iteration of the loop. Now draw a pipeline diagram illustrating the second iteration of the loop. Clearly indicate the number of cycles it takes to execute the second iteration. Calculate the CPI for this processor executing all 64 iteration of the loop (Note: The CPI calculation should not include instructions that are fetched but then later squashed).