Reference no: EM13194927
1. Information about two diversified risky portfolios is given in the Table below:

a. Assuming a risk-free rate of 5%, calculate the Sharpe ratio for P1 and for P2. Which portfolio is likely to be the Market Portfolio, PM? Explain briefly the rationale for your answer.
b. Consider the portfolio you have chosen in (a) as the market portfolio. (If you have not been able to answer part a, use one of P1 or P2 as the market portfolio for subsequent questions). Consider the following asset:

Determine the beta coefficient (βA) for stock A. Is stock A fairly priced, undervalued or overvalued according to CAPM? If Stock A is undervalued or overvalued, indicate by how much. Explain your answer.
2. Stock A has an expected return of 12% and β = 1. Stock B has an expected return of 13% and β = 1.5. The market's expected return is 11% and rf = 5%.
a) What is the alpha of each stock? Compare each stock's risk-return point graphically and identify each alpha clearly.
b) According to the CAPM, which stock is a better buy? Explain your answer.
3. A risk-averse investor has a preference function that may be written as where E[r] is the expected rate of return as
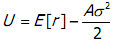
,E(r) is the portfolio variance and A is the degree of risk aversion which you are told is equal to 1.5. The investor is considering the formation of a portfolio comprising two independent risky assets, A and B, and a risk-free asset, G, that can be lent or borrowed at a constant risk-free rate of 2.5%.
Risky asset A offers a return of 12% and has a standard deviation on return of 4%; risky asset B offers a return of 16% and has a standard deviation on return of 5%.
a) In what proportions should the investor hold his wealth?
b) Using a diagram to illustrate your answer, explain the key element of the method used by the investor to solve the portfolio problem.
4. Suppose that the expected rate of return on an efficient market portfolio is 20% and the rate of return on the risk-free asset is 8%. The standard deviation of the market portfolio is 32%.
a) What is the equation for the Capital Market Line? Explain your answer and interpret this relationship.
b) If an expected rate of return of 17% was required, what is the standard deviation of this position?
c) If you have £1000 to invest, how should you allocate your funds to achieve this position? Explain your answer.
d) If you invest £300 in the risk-free asset and £700 in the market portfolio, what is the expected value of the portfolio at the end of the year?
e) Suppose that an asset with a return of 17% and a standard deviation of 24% exists that is correlated, ρ = 0.4 with the market. What is the beta of this asset? Interpret your result.
5. The Finance Director of a company is considering an investment in a new production line. The investment will cost £200 million today and a further £50 million in one year's time. The Finance Director believes that the revenue stream from the investment will depend upon the state of the economy as described in the Table below, where Year 0 is the present day.
If the discount rate is 4%, what is the present value of the project?
