Reference no: EM133814866

1. Cryptanalysis of the One-Time Pad

For this question, you need the encrypted ciphertexts downloaded from LEARN. There will be 3 blocks of ciphertexts. These were all encrypted with a one-time pad; however, they were all encrypted using the same key. You know that they are English language text in the utf8 encoding.

Give the plaintext messages which were encrypted.

Describe the methods you used to break this encryption (if you used computer code, attach any code as a PDF or image).

(There is no set marking scheme for this: it is mainly a chance to show your work).

2. Rationale of SPN Ciphers
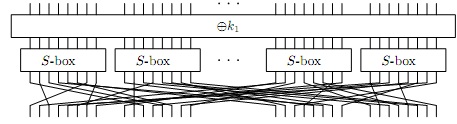
Recall the basic construction of an SPN cipher: It proceeds through "rounds": where each round updates an internal state c with the following operations:
a) XOR the ith key onto c
b) Apply an S-Box to each byte of c
c) Apply the permutation P to c

This is illustrated below:

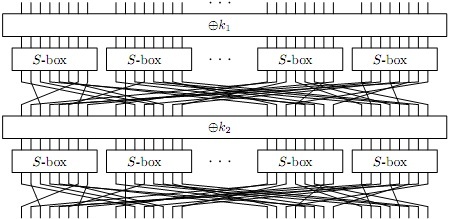
(for as many rounds as required).
In this question we will consider why this structure breaks completely if any one of the operations is removed.

For all of the modifications below, describe an effective attack against the encryption, more powerful than an indistinguishability attack.
All of your attacks should have complexity significantly lower than a brute-force key search. For all attacks, you must state the 3 components of the security model you have broken: what is the adversary's goal, what is the adversary's communication capability, and what is the computational power of the adversary? Get your questions answered now!

Assume the original SPN cipher is secure, i.e., this is a good S-box, a good permutation, and the key scheduling is secure.

If necessary, assume the S-box takes 8-bit inputs, the block length is 128 bits, the key length is 128 bits, and there are 16 rounds.
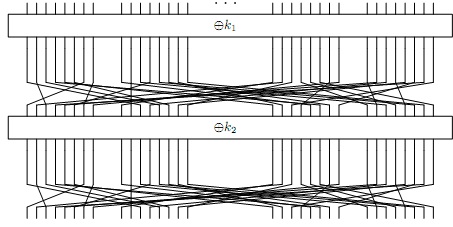
Suppose the permutation is removed, as shown below:

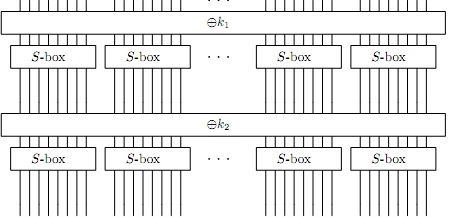
Suppose the S-box is removed, as illustrated below:

Suppose the key is not XORed into each round, as illustrated below:

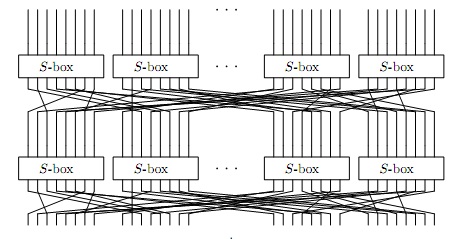
Suppose the SPN only applies one round, as illustrated below:

(Assume no whitening key is used at the end; for 1 bonus mark, describe an attack on a one-round SPN that does use a whitening key.)

3. Stream Ciphers
Suppose G is a secure pseudorandom bit generator, and we naively build a stream cipher as follows: Encrypt(k, m):
Select a random IV
Input k and IV into the PRBG to obtain a random string k′ as long as the message.
Output (IV,k′ ⊕ m).
Decrypt(k, (IV, c)):
Input k and IV into the PRBG to obtain a random string k′ as long as the ciphertext.
Output k′ ⊕ c.
Suppose the PRBG is secure. Show that this scheme is not IND-CCA secure.