Reference no: EM132052451
Assignment - Graph Theory
Question 1: Determine and graph the location of a central warehouse which minimizes Distance times Volume weighted costs on a geographic graph for the following individual facilities. Graph the actual unweighted geographic coordinates of Facilities 1-5, and the optimally weighted location of the central warehouse.
| Facility |
East |
North |
Volume |
| 1 |
8 |
10 |
7 |
| 2 |
5 |
3 |
4 |
| 3 |
10 |
5 |
10 |
| 4 |
1 |
10 |
4 |
| 5 |
2 |
5 |
1 |
Question 2: Figure and Table below provides the complete (symmetric) network transportation costs between the nodes (A to F) of a logistical network. Use the Nearest Neighbor heuristic to find a low-cost tour that visits each node exactly once, starting with point A. Report the tour sequence and total distance. Show the steps of your iterations. (Not drawn to scale.)
| Cost |
A |
B |
C |
D |
E |
F |
| A |
- |
24 |
85 |
57 |
84 |
66 |
| B |
24 |
- |
71 |
53 |
65 |
49 |
| C |
85 |
71 |
- |
47 |
57 |
68 |
| D |
57 |
53 |
47 |
- |
89 |
83 |
| E |
84 |
65 |
57 |
89 |
- |
18 |
| F |
66 |
49 |
68 |
83 |
18 |
- |
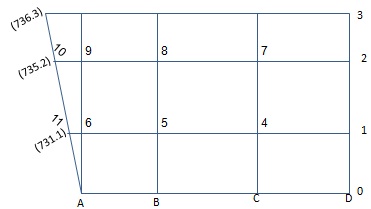
Question 3: Use the same Figure and Table with the Cheapest Insertion Point heuristic to find a low-cost tour visiting each node exactly once.
Report tour sequence and total distance. (Remember to start with the longest double-arc.) Show the steps of your iterations.
Question 4. What is Maximum flow in Graph below?
Question 5. What is the Minimum Spaning Tree (MST) in Graph?
Question 6. Write down the Vertex names of your Min Cut; e.g., AB, AC, etc.
Question 7. Write down the Vertex names of your MST; e.g., AB, BC, etc.
Attachment:- Assignment.rar