Reference no: EM13212471

1. Choose between A and B (circle your choice on the hard copy, and enter A or B in the spreadsheet table), where

- A = a guaranteed loss of $750

- B = 25% chance to lose nothing, 75% chance to lose $1000

2. Imagine that you face the following choice. You can accept a guaranteed $1,500 or accept a stylized risk. The outcome of the stylized risk is determined by the toss of a fair coin. If heads comes up, you win $1,950. If tails comes up, you win $1,050. Which would you choose?

- C = the guaranteed $1,500

- D = the 50-50 risk of winning $1,950 or winning $1,050

3. Imagine that you face the following choice. You can accept a guaranteed loss of $750 or accept a stylized risk. The outcome of the stylized risk is determined by the toss of a fair coin. If heads comes up, you lose $525. If tails comes up, you lose $975. Which would you choose?

- E = the guaranteed loss of $750

- F = the 50-50 risk of losing $525 or losing $975

4. Imagine that you are in a situation where 75% of the time you lose $760. And 25% of the time you win $240. It's an unavoidable risk you have to take. Now I give you a choice. Which would you choose?

- G = face the risk I just described and in addition I'll give you $10

- H = face the risk I just described and instead of giving you $10, I'll give you $0

5. This question concerns how your attitude to risk depends on other aspects of your financial situation. Imagine that you have just won $1,500 in one stylized lottery, and have the opportunity to participate in a second stylized lottery. The outcome of the second lottery is determined by the toss of a fair coin. If heads comes up, you win $450 in the second lottery. If tails comes up, you lose $450. Which would you choose?

- I = accept the 50-50 risk of winning $450 or losing $450

- J = reject the 50-50 risk of winning $450 or losing $450

6. Imagine that you have just lost $750 in one stylized lottery, but have the opportunity to participate in a second stylized lottery. The outcome of the second lottery is determined by the toss of a fair coin. If heads comes up, you win $225 in the second lottery. If tails comes up, you lose $225. Which would you choose?

- K = accept the 50-50 risk of winning $225 or losing $225

- L = reject the 50-50 risk of winning $225 or losing $225

7. Consider a decision task featuring choice from a set of two alternatives M and N with the same expected payoffs. Which would you choose?

- M = a sure loss of $500

- N = a 50-50 risk where you will either lose $1000 or lose $0

8. Consider a decision task featuring choice from a set of two alternatives O and P with the same expected payoffs. Which would you choose?

- O = a sure loss of $500

- P = a 2:1 risk where you will either lose $1000 with probability 1/3 or lose $250 with probability 2/3

9. Imagine that you have a choice among two alternatives. Your first alternative is to accept $150 immediately. Your second alternative is to accept possibly a different amount of money at a future date.

9.1. If you had to wait one month, instead of receiving $150 immediately, what is the lowest amount of money that you would consider accepting?

9.2. If you had to wait 12 months, instead of receiving $150 immediately, what is the lowest amount of money that you would consider accepting?

9.3. If you had to wait 10 years, instead of receiving $150 immediately, what is the lowest amount of money that you would consider accepting?

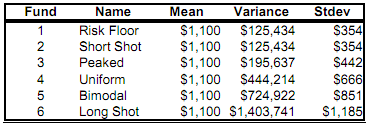
10. In question 21 of the course questionnaire, you were asked to imagine a situation where you have an opportunity to choose from among six different funds. As was the case in question 21, these funds have to be held for a period of one year. The six charts that appear on the following pages provide the probability distribution for what each of the funds will be worth after you have held them for a year. Before the charts, you will also see a table that shows the mean, variance, and standard deviation for what each fund will be worth after a year.

Examine all six charts and then answer the following question.

Suppose these are funds you have to buy, not funds you receive as part of a bonus. For each fund, what is the minimum expected return you feel you would require in order to be willing to buy that fund, and hold it for a year? Because there are six funds, your answer will consist of six minimum required returns.

The data table is below and the charts begin on the next page.

Attachment:- Exercise.pdf