Reference no: EM133306456

Part A This part consists of six questions. Answer all questions.

Question 1
a) An attacker compromised a system of internal network from a remote place. Then, the compromised system has been used to redirect all packets destined to a web server. Identify the type of attacks launched by the attacker. Explain the attack scenario with figure.

b) The following text is the output of CAESAR cipher: Wigyvmxc. Find out the key and the corresponding plaintext.

Question 2
Suppose, you are the administrator of an information system where every registered user can access the public keys of any other users. Alice and Bob are registered users of the system. Now, as part of a business process, Alice wants to send sensitive data to Bob using a symmetric-key encryption scheme. However, Alice and Bob do not share any secret key currently. They do not have any secure physical channel which can be used to exchange secret keys safely without encryption. Given the constraints, is it possible for Alice and Bob to exchange sensitive data using a symmetric-key encryption? If possible, explain how.

b) What are the four ways used to distribute public key?

Question 3
a) Suppose, a network consists of four different nodes (A, B, C and D). How many keys do they have to generate such that A, B and C can communicate with D in a bidirectional secure way using the DES algorithm? How many keys do they have to generate such that every pair of nodes can communicate in a bidirectional secure way using the same algorithm? How many keys do they need to generate for both scenarios while using 3DES algorithm?

b) Symmetric encryptions (e.g., AES) can provide data confidentiality like public-key algorithms. What are the two issues that can mainly be addressed by public-key cryptography? Justify your answer in brief.

Question 4
a) Suppose, an LFSR has the following feedback polynomial function: 1 + X² + X³. Draw the LFSR and also find the bit stream period to determine whether the function is a primitive polynomial.

b) What are the different ways to identify abnormal network behaviour? List at least four of them.

Question 5
a) Compare and contrast with figures between application-level gateway and circuit-level gateway firewalls.

b) What are the two ways to protect password files?

Question 6
a) The following table shows a couple of encryption algorithms and their key sizes employed by TLS and WTLS:

Algorithm	TLS Key Size (bits)	WTLS Key Size (bits)
3DES	168	40
IDEA	128	40 or 56

Explain why in these cases for the same algorithms WTLS uses shorter keys.

b) Consider a commercial information system which supports data transmission between peer users and between servers and users on the Internet. The system administration team is concerned on data integrity in their servers. Name an access control model, which can be used to protect data integrity. Explain how the model works.

c) How does the recipient in PGP identify the public key of sender?

Part B
This part consists of twoquestions. Answer all questions.

Question 1

a) Consider an application based on wireless communications, which requires a session key of length 15 (that is, 15 bits). For the key to be robust against any brute-force attack, it is required that the session key does not contain any repeating patterns. The following is a linear feedback shift register (LFSR)of length 4. Answer the following questions:

 

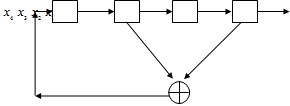
Given the initial bits x₁=1, x₂=1, x₃=0, and x₄=1,can a session key that meets the above security requirement be produced by this LFSR? If so, write the first 15 bits of the output stream of the above LFSR. If not, find the period of the output stream.

b) Write a program in shell script that will take an integer value from the useras input and check whether the number is odd or even. The program should continue forn times. See below the sample input and output of the program.

How many times you want to enter the number? 3
Number 1: 10
It is an even number!
Number 2: 7
It is an odd number!
Number 3: 0
Please enter a number greater than 0.

Question 2

a) Suppose the alphabet for creating passwords consists of 10 characters. Without loss of generality, we denote it as A = (a₁, a₂,a₃,a₄,a₅,a₆,a₇,a₈,a₉,a₁₀). Suppose each password must contain 8 characters. How many potential passwords do we have?

b) Suppose among all potential passwords, 1% of them can be viewed as "bad passwords". Given a password, to check whether or not it is a good password, we can compare it with all the "bad passwords" one-by-one. Using this procedure, how many comparisons do we have to operate in the worst case?

c) Given the dictionary of "bad passwords", which is denoted as D, consisting of all the "bad passwords", suppose the matrix of transition probability of a Markov model is given as

 

where the entry at row i and column j in the above matrix, T(i, j), represents the probability that the character a_i is followed by a_j in the dictionary, that is, the frequency of the occurrence of the bigram a_ia_j in the dictionary of "bad passwords". Now, you are given a password, a₁a₂a₄a₁a₁₀a₅a₃a₁. Is this a good password? Explain.

d) The Hamming distance between two points, (x₁, x₂, K, x_n) and (y₁, y₂, K, y_n), is defined as:

d_H(x₁, x₂,,.....x_n),(y₁,y₂,......y_n))=#{i; x_i≠y_i}

that is, the number of coordinates where (x₁, x₂, K, x_n)and(y₁, y₂, K, y_n)differ. Given the following data items which are points in the 4-dimensional space, for each pair of data items, calculate the Hamming distance between them:

(1,0,1,0), (1,1,1,0), (1,0,0,0), (0,1,0,1)

Which data point is the most distant one from other data points with respect to the Hamming distance?