What are the initial and final tensions in the string

Reference no: EM13811129

1. A small block on a frictionless surface has a mass of 70 g. It is attached to a massless string passing through a hole in a horizontal surface.

The block is originally rotating in a circle of radius 45 cm with angular speed 0.80 rad/s. The string is then pulled from below until the radius of the circle is 25 cm. You may treat the block as a point particle.

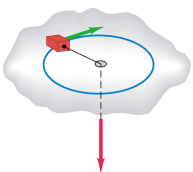
2016_Is the angular momentum of the block conserved.png

(a) Is the angular momentum of the block conserved? Why or why not?

(b) What is the final angular speed?

(d) What was the change in kinetic energy of the block?

(e) How much work was done in pulling the string?

2. A diver stands on the end of a diving board as shown in the figure on the right. The mass of the diver is 58 kg and the mass of the uniform diving board is 35 kg.

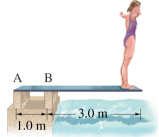
1528_Is the angular momentum of the block conserved1.png

Calculate the magnitudes and directions of the forces exerted on the board at the points A and B.

3 A ladder, 5.0 m long, leans against a frictionless wall at a point 4.0 m above the ground. A painter is climbing up the ladder. The mass of the ladder is 12.0 kg and the mass of the painter is 60.0 kg.

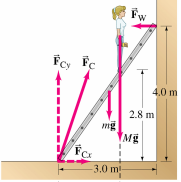
493_Is the angular momentum of the block conserved2.png

The ladder begins to slip at its base when the painter is 70 % of the way up the length of the ladder. What is the coefficient of static friction between the ladder and the floor?

4 You are doing exercises on a Nautilus machine in a gym to strengthen your deltoid (shoulder) muscles. Your arms are raised vertically and can pivot around the shoulder joint, and you grasp the cable of the machine in your hand 64.0 cm from your shoulder joint. The deltoid muscle is attached to the humerus 16.0 cm from the shoulder joint and makes a 12.0° angle with that bone.

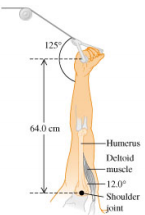
2197_Is the angular momentum of the block conserved3.png

a) If you have set the tension in the cable of the machine to 33.0 N on each arm, what is the tension in each deltoid muscle if you hold your outstretched arms in place?

b) What then is the magnitude of the force on the humerus bone at the shoulder joint if you are holding your arm in place? (Assume the mass of the arm is 8.0 kg.)

Reference no: EM13811129

Questions Cloud

Determine the output displayed in the text box : For each of the responses shown in the parentheses, determine the output displayed in the text box when the button is clicked

Write a program that asks for the amount of the bill : Write a program that asks for the amount of the bill and percentage tip and calculates the tip. The program should use variables for each of the quantities and display the outcome in a text box with a label. Test the program on a bill of $20 and a..

What is cultural geography or human geography : What is Cultural geography or Human Geography

What is the magnitude of the workers displacement : A worker leaves home at 9:00 AM, travels 40 km to the office, and then returns home at 5:00 PM. What is the magnitude of the worker's displacement during this 8-hour span of time?

What are the initial and final tensions in the string : Is the angular momentum of the block conserved - what is the final angular speed and What are the initial and final tensions in the string.

The organization of economic activity from the control : By removing the organization of economic activity from the control of political authority, the market eliminates this source of coercive power. It enables economic strength to be a check to political power

Manufacturing and service industries : Prepare a two-page paper based on "Manufacturing and Service Industries."

Creating-sustaining an innovative organizational culture : Prepare a two-page paper on "Creating and Sustaining an Innovative Organizational Culture."

Overweight and obesity : Overweight and Obesity

User Account

All Pages