What about the lateral transfer of a force

Reference no: EM13809127

Question 1:

"Time has no beginning and it has no end". Do you agree that, true or false, this statement is of no practical concern to an engineer? Give your reason(s).

Question 2:

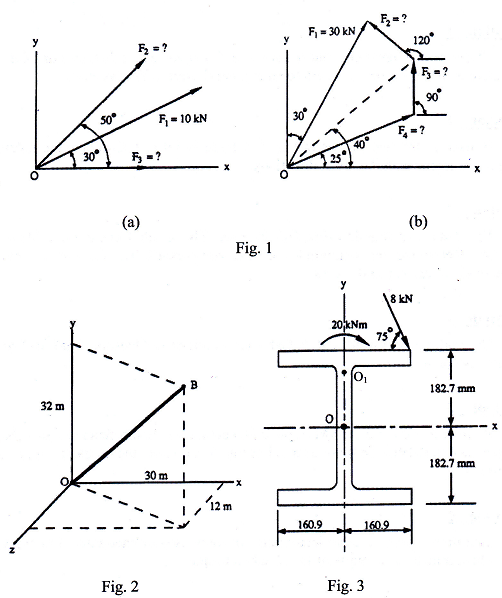
In each of the two figures in Fig. 1, a force is defined. Compute the unknown component forces with the given directions.

Question 3:

Fig. 2 shows a straight cable, OB, in space. The tensile force in the cable is T = 100 kN. Determine the magnitudes of the components Tx, Ty, and T2 parallel respectively to the x, y and z axes.

Question 4:

By working backward, check that your solutions to Question 2 do lead to the correct resultants

Question 5:

A force F and a moment M (around 01) acting on the top flange of an I-shaped column section (310UC283) are detailed in Fig. 3. Compute the moment with respect to point 0.

Question 6:

Cite three examples from instruments or tools used or encountered in everyday lives which transform a couple of forces into a torque.

Question 7:

Translating the point of action of a force along its line of action does not affect the movement of a structure (which may be considered as an elastic body). However, it does affect the local deformation and internal forces. What about the lateral transfer of a force on the same structure?

Question 8:

Inspect the building in which you live and recognise the various structural elements and the types of loading they carry.

1737_Compute the unknown component forces.png

Part 2:

Question 1:

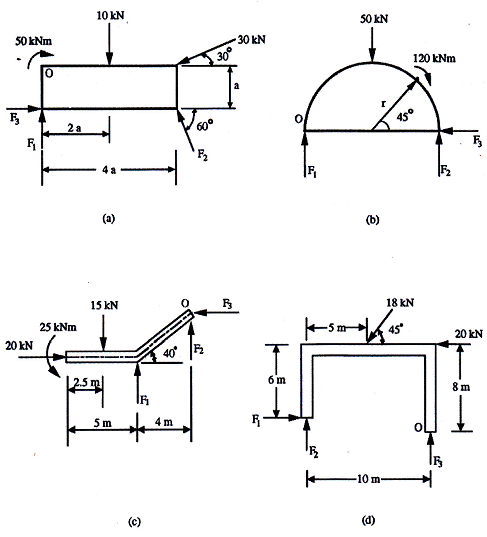
For each of the planar systems shown in Fig. 1, set up, quantitatively, the relevant equilibrium equations, IF„ = 0, IFy = 0 and EM = 0. Note that the moment equations should be with respect to point 0 as indicated. Also compute F1, F2 and F3.

717_Compute the unknown component forces1.png

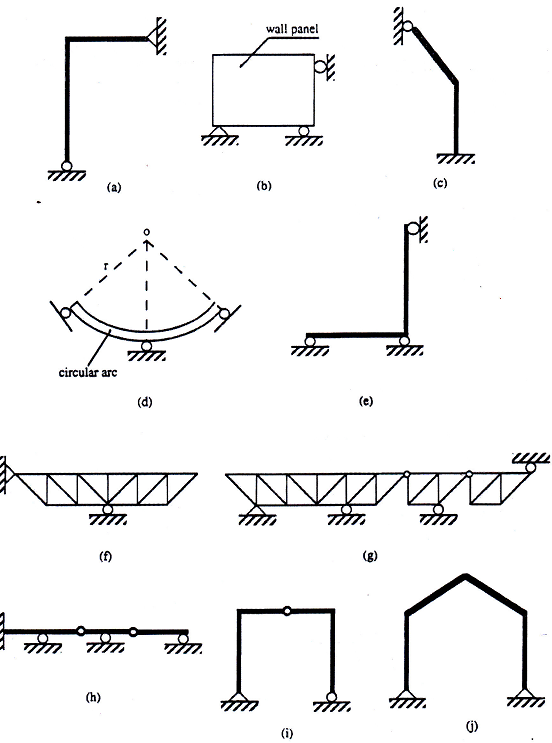
TUTORIAL 3: SUPPORTS AND SUPPORT REACTIONS

Question 1:

Consider each of the planar structures illustrated in Fig. 1 and determine if it is statically determinate, externally. If it is not, is it unstable or statically indeterminate?

Question 2:

Fig. 2 shows details of the centre-line diagrams for a number of beams, trusses, arches and frames which are externally determinate. Compute the support reactions.

Question 3:

For each of the continuous structures with internal hinged-connections as detailed in Fig. 3, determine the support reactions.

Question 4:

Using the graphical method, repeat Questions 2(c), 2(f), and 3(a).

2057_Compute the unknown component forces2.png

Reference no: EM13809127

Questions Cloud

Analyze the proposal adequacy for organizing a proposal : Analyze the proposal adequacy checklist for organizing a proposal, and summarize the intrinsic value of two (2) of the suggestions on the checklist. Prepare and articulate an argument in support of your position.

Calculate the total cost using a one-month planning horizon : Calculate the total cost using a one-month planning horizon. Calculate the total cost using a three-month planning horizon.

Archiving cost and schedule data for projects : Determine one (1) mistake that project managers are most likely to make when archiving cost and schedule data for their projects. Next, propose one (1) strategy or best practice for limiting the mistake in question. Justify your response.

Presentation on comparing and contrasting operations : You have been asked to develop a short presentation on comparing and contrasting operations management to supply chain management.

What about the lateral transfer of a force : Affect the local deformation and internal forces. What about the lateral transfer of a force on the same structure?

Reflect on the events leading up to the dhs : Reflect on the events leading up to the DHS, the current state of the DHS; and the future of DHS. What changes will need to be implemented to address the future of DHS.

Comparing and contrasting operations management : You have been asked to develop a short presentation on comparing and contrasting operations management to supply chain management.

Explain the threat posed by the group profiled : Use the group profile to conduct an analysis of one or more U.S. homeland security policies studied in module 2, to assess the ability of the policy or policies to counter the threat posed by the group profiled.

Describe the motivation for the paper : Introduction/Overview: Describe the motivation for the paper, clearly state the research you are conducting, and identify your reasons for choosing the particular papers you chose.

User Account

All Pages