Use this to check the fit of the model

Reference no: EM131038491

Problem 4.1 with Table 4.8 used a labeling index (LI) to predict π = the probability of remission in cancer patients.
When the data for the 27 subjects are 14 binomial observations (for the 14 distinct levels of LI), the deviance for this model is 15.7 with df = 12. Is it appropriate to use this to check the fit of the model? Why or why not? b. The model that also has a quadratic term for LI has deviance = 11.8. Conduct a test comparing the two models. c. The model in (b) has fit, logit() = -13.096 + 0.9625(LI) - 0.0160(LI)2, with SE = 0.0095 for 2 = -0.0160. If you know basic calculus, explain why is increasing for LI between 0 and 30. Since LI varies between 8 and 38 in this sample, the estimated effect of LI is positive over most of its observed values. d. For the model with only the linear term, the Hosmer-Lemeshow test statistic = 6.6 with df = 6. Interpret.

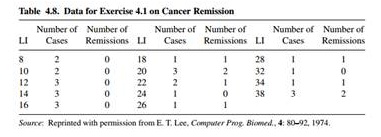
Problem 4.1 A study used logistic regression to determine characteristics associated with Y = whether a cancer patient achieved remission (1 = yes). The most important explanatory variable was a labeling index (LI) that measures proliferative activity of cells after a patient receives an injection of tritiated thymidine. It represents the percentage of cells that are "labeled." Table 4.8 shows the grouped data. Software reports Table 4.9 for a logistic regression model using LI to predict π = P(Y = 1).

a. Show how software obtained πˆ = 0.068 when LI = 8.

b. Show that = 0.50 when LI = 26.0.

c. Show that the rate of change in is 0.009 when LI = 8 and is 0.036 when LI = 26.

d. The lower quartile and upper quartile for LI are 14 and 28. Show that πˆ increases by 0.42, from 0.15 to 0.57, between those values.

e. When LI increases by 1, show the estimated odds of remission multiply by 1.16.

Reference no: EM131038491

Questions Cloud

Estimate of the after-tax cost of debt : The noncallable $1,000 par value, 20-year, 7.25% bonds with semiannual payments are selling for $875. The firm's tax rate is 40%.

Calculate the value of a bond that matures : Question 1:(Bond valuation) Calculate the value of a bond that matures in 12 years and has $1,000 par value. The annual coupon interest rate is 9 percent and the market's required yield to maturity on a comparable-risk bond is 12 percent. Round to..

Why did japan commit atrocities against the chinese : How did Gandhis independence movement succeed against the British in the 1920s and 1930s - Why did Japan commit atrocities against the Chinese in Nanjing in 1938?

Write an research essay about the danger of a single story : Write an Research Essay about The Danger of a Single Story. we have had an opportunity to view and discuss several TED talks that explore social problems and questions of identity.

Use this to check the fit of the model : When the data for the 27 subjects are 14 binomial observations (for the 14 distinct levels of LI), the deviance for this model is 15.7 with df = 12. Is it appropriate to use this to check the fit of the model? Why or why not? b. The model that als..

Were conclusions well grounded in the findings : What were the main findings of the research? Were the results substantively important?

Discuss the elements necessary to form a valid contract : Evaluate the potential remedies for breach of contract that might be available if someone breached the contract clause you created.

Pocket margin associated with the customer : Assuming cost of capital is 12% then what is the pocket margin associated with the customer?

Explain how this table was constructed : Refer to the classification table in Table 5.3 with π0 = 0.50. a. Explain how this table was constructed.

User Account

All Pages