Reference no: EM131130140

Calculus Assignment - Title: Problem Solving- Infinite Limits and Derivatives

1. Use the graph of the function to determine the limit lim_x→3f(x), if exists.

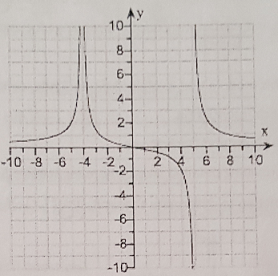
2. The graph of shown below has vertical asymptotes at x = -4 and x = 5. Find the following. Use  ∞ or -∞ when appropriate.

a. limx→_-4^- f(x)    

b. lim_x→4^+ f(x)

c. lim_x→-4 f(x)

d. lim_x→5^- f(x)

e. lim_x→5^+ f(x)

f. lim_x→5 f(x)

3. Find the limit.

lim_x→4^+ 4/x-4

4. Evaluate the limit, using ∞ or -∞ when appropriate, or state that it does not exist.

lim_x→1(5x²-5/x-1)   

5. Find all vertical asymptotes, x = a, of the function f(x) = (x³-9x²+14x/x²-7x). For each value of a evaluate lim_x→a^+ f(x), lim_x→a^-f(x), and lim_x→a f(x). Use ∞ or -∞ when appropriate.

6. Find all limit of the rational function h(x) = (16x³/13x³+15x²+11x) when:

a. X → ∞

b. X → -∞

7. Evaluate lim_x→∞f(x) and lim_x→-∞f(x) for the function f(x) = (x³+8/4x³+√(64x⁶+4)). Use ∞ or -∞ where appropriate. Then give the horizontal asymptote(s) of f (if any).

8. If a function f represents a system that varies in time, the existence of lim_t→∞f(t) means that the system reaches a steady state (or equilibrium). For the system of the population of a culture of tumor cells given by p(t) = 3400t/t+2, determine if a state exists and give the steady-state value.

9. What is the domain of f(x) = √(1-x²) and where is f continuous?

10. State whether the indicated function is continuous at 4.

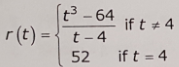
11.   Suppose f(x) is defined as shown below.

a. Use the continuity checklist to show that f is not continuous at 0.

b. Is f continuous from the left or right at 0?

c. State the interval(s) of continuity.

12. Determine the interval(s) on which the following function is continuous. Be sure to consider right-and left-continuity at the endpoints.

f(x) = √(3x² - 24)  

13. Evaluate the following limit.

lim_x→3π/2(sin² x + 5 sin x + 4/sin x + 1)

14. Use the Intermediate Value Theorem to verify that the following equation has three solutions on the interval (0, 1). Use a graphing utility to find the approximate roots.

140x³ - 139x² + 38x - 3 = 0.