Reference no: EM131851340

Question 1. Ortho-normal condition of the scattering states

Using the Lippmann-Schwinger(LS) equation:

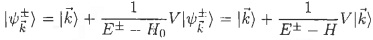                          (1)

to show that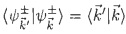 

Question 2. The Feymann propagator and Green function:

(a) Using a suitably chosen contour-integral to show:

-1/2Πi _-∞∫^∞ dE e^-iE(t-to)/h/(E⁺- E₀) = 0(t - t₀)e^{-iE0(t - t0)/h}

(b) Using the above equation to show that the Feymann propagator K(r^→, r^→'; t, t₀) = θ(t - t₀)(r^→|e^{-iH(t - to)/h}|r^→') can be expressed in terms of the Green functions as:

K(r^→, r^→'; t, t₀) = i/2Π. 2μ/h²_-∞∫^∞ dE e^-iE(t-to)/hG⁺_E(r^→, r^→')

where G⁺_E(r^→, r^→') is the retarded Green function

Question 3. The Born approximation

The charge density ρ(r^→) = ρ₁(r^→) + ρ₂(r^→) with ρ₁(r^→) = eδ(r^→) and can ρ₂(r^→) = -c/(4Πa²).δ(r-a) can be thought of as a very crude description of the distribution of charge in a naive model of the hydrogen atom with the proton located at the origin, assumed to be infinitely small and the electron located in an infinitely thin spherical surface of radius a. Let dσ/dΩ and dσ₁/dΩ denote the differential cross sections describing the scattering of a particle of charge e from the electrostatic potentials due to p(r^→) and p(r^→) respectively.

(a) Use the first Born approximation to calculate the ratio R(E, θ) = (dσ/dΩ)/(dσ₁/dΩ) and find the limit of R(E, θ) as E → ∞ and E → 0. In the E → 0 limit, consider terms up to E² in the low energy expansion.

(b) In a more realistic description, p₂(r^→) is determined by the probability distribution of the electron in the ground state of the hydrogen atom. Repeat the calculation of R(E, θ) as described in (a); study the same limiting cases and contrast the qualitative behavior of R(E, θ).

(c) Consider a one dimensional scattering of a particle by the real potentials V(x) = g₁δ(x -a) +g₂δ(x) + g₃δ(x + a) and V(x) = g₃δ(x - a) + g₁δ(x + a). The interaction strengths g_i are different from each other and the particle is incident from the left on both cases. Let T and T be the transmission coefficients for V and V' respectively. Write down an exact relation of T - T'.

(d) Use the Born approximation to calculate the reflection coefficients R and R'. Assuming g₁ = g₂ = g₃, discuss the possible appearance of diffraction maxima in T.

Question 4. Studying the 1d scattering problem by solving Schrodinger equation directly.

Consider a particle scattered by a one-dimensional potential V(x) such that V(x) = 0 for |x| > a > 0.

(a) Show that in the regime lx| > a and with an appropriate choice of an overall normalization constant, the solution can be written as:

ψ_λk = e^iλkx + ∫(k', λk)e^ik|x|

where k = √(2mE)/h > 0, k' = x/|x|k and λ = ± represents incidence from the left/right.

(b) Prove that ψ_k and ψ_-k are orthogonal.

From now on assume that V(x) = gδ(x).

(c) Calculate the scattering amplitude f (k', λk) for all values of λ and k'.

(d) Calculate the quantity

∑_{λ 0}∫^∞dk/2Πψ_λk (x)ψ*_λk(x')

and compare your result with what is expected from the completeness relation

∑_n ψ_n (x)ψ*_n(x') = δ(x - x') 

Question 5. Studying the 1d scattering problem by using the 1d Green function.

The positive-energy stationary solution of the Schrodinger equation describing a particle scattered by a one dimensional potential V(x) are determined by the equation:

(d²/dx² + k²) ψ_λk(x) = 2m/h²V(x)ψ_λk(x)

where λ and k are defined in the previous problem and the potential is assumned to vanish for |x| > a.

(a) Show that ψλk(X) can be written as

ψ_λk(x) = e^iλkx + 2m/h² _-∞∫^∞dx'G(x - x')V(x')ψ_λk(x')

where G(x) satisfy:

(d²/dx² + k²) G(x) = δ(x)

(b) Find G(x) which represents outgoing waves, namely, proportional to e^ik|x|

(c) Write clown G(x - x') in the limit |x| >> |x'| and show that for |x| >> a:

ψ_λk = e^iλkx + f(k', λk)e^iλk|x|

where k' = x/|x|.k

(d) Assume that V(x) = gδ(x), solve the integral equation for ψ_λk(x) and compare with the result found in the previous problem by solving the same 1d scattering problem directly without using the Green function.

(e) Show that the total Green function Gt(x) which satisfies the equation:

(d/dx² + k² -2m/h² V(x))G_t(x) = δ(x)

is related to G(x) by:

G_t(x, x') = G(x - x') + 2m/h² _-∞∫^∞ dx''G(x - x'')V(x'')G_t(x'', x')

(f) Let V(x) = gδ(x), solve the integral equation of part (e) and determine the explicit form of G_t(x, x'). Please also answer the following physical questions: Is Gt(x, x') translational invariant ? namely, can one write Gt(x, x') = G_t(x - x') which only depends on the difference x - x' just like the non-interacting Green function G(x - x') ?

Question 6. Solving a 1d scattering problem with non-local separable potential

A particle of mass m moving in one dimension is scattered by the non-local potential (x'lVlx) = gv(x')v(x) where v(x) is a real monotonic function that vanishes faster than 1/x at infinity. In the special case of v(x) = gδ(x - x₀), calculate both the transition amplitude and the full Green's function in the x representation, i.e, find:

(x'|V + V(1/E⁺ - H).V|x);  (x'|1/|E⁺ - H|x)

Hint: It may be constructive to compare with the single δ(x) potential problem discussed in the last problem.