Reference no: EM13371834

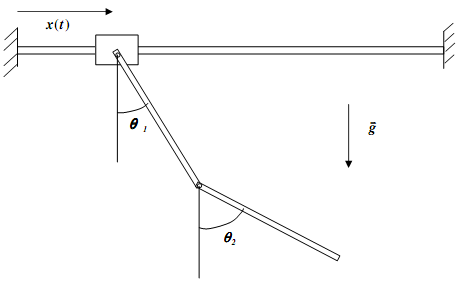
This project involes determining the dynamics of the double pendulum with a sliding base (see figure above). Each link is assumed to be of square cross section.

The objective is to determine the angles θ₁ and θ₂ over the time period of t = 0 s to t = 4 s. Let the base motion be prescribed as x(t)= 1/8 sin(4.2t). Based on the Newton's second law, the equations of motion (for the angular acceleration of each link) are given by

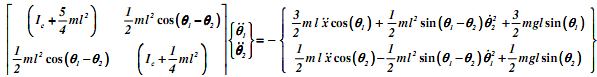
where m and l are the mass and length of the links and I_c = ml²/12 is the moment of inertia of each link. Important note: the 'dot' notation over the symbol means the corresponding derivative with respect to time.

The values of various parameters to be used in the calculations are:

g = 9.81 m/s²; I = 0.50 m; p = 6500 kg/m³ (link density); b = .05 m (dimension of square link cross-section); m =1*(b*b)op kg; l_c = m*I*1/12.0 m³.

The above is a system of two 2^nd order ordinary differential equations (ODEs). In order to be able to solve this, first transform them into an equivalent four 1^st order ODEs. This can be accomplished as follows: Inverting or solving the system of equations above (using the backslash operator or other techniques in MATLAB) and using the fact that dθ₁/ dt = ^.θ₁ d^.θ₁/dt = ^..θ₁ (and similarly for θ₂ ) will provide the values needed to complete the right hand side of the following representation of the system of four 1^st order ODEs

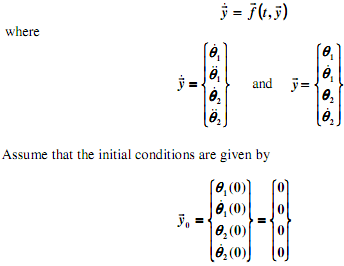
Write a MATLAB program that solves for y' over the interval t = 0 s to t = 4 s using three different methods: the Euler method, the mid-point method (2^nd Order Runge­Kutta), and the classical 4^th Order Runge-Kutta method.

To evaluate the effect of your step size (h) on the results for each of the three methods, use the following six values of h (units of seconds): 0.02, 0.01, 0.005, 0.0025, 0.00125, and 0.000625. For step sizes 0.01s and smaller, calculate the approximate percent relative error in θ₁ at t = 4 s between the current step size and the next largest step size.

For example, for a step size of 0.01, the approximate percent relative error is: