The set of all permutations over the group formsunder

Reference no: EM1318734

Question: Group theory is a wide, autonomous area of mathematics which affects almost any other area of pure mathematics. For computer science is of importance too. It is fundamental for areas such as Computational Complexity, Algorithm, Cryptography, & Combonatorics to name a few. The rest of this question focuses on some particular groups, known as permutation groups.

Fix a set Ω = {1, 2, 3,....., n}. A permutation π on Ω is a bijection (1-1 & onto), π : Ω® Ω. Observe that the composition of two permutations is also a permutation. Here is a convenient way to denote permutations. Example {in this notation same column element from the first row are mapped to the corresponding element of the second row}:

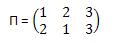
Answer the following:
Fix n € N. Show that the set of sn of all permutations over [1, 2,........n] forms a group under the operation of composition. That is, show that composition is a binary operation over the set of permutations, & the three axioms - mentioned above - are satisfied.

Reference no: EM1318734

Questions Cloud

Make a cycle decomposition : Make a cycle decomposition

Estimation of confidence interval for r-square : If we want to increase our confidence level from 95% to 99%, what happens to our confidence interval?

Stepwise regression model summary : A researcher used stepwise regression to create regression models to predict Birthrate (births per 1000) using five predictors:

Pertinent issues involved in following facts : Identify all of the pertinent issues involved in following facts. Apply the rules of law to the problems and describe what your decision will be as judge for a day. Support your answer clearly with reasons. Explain why. (Three points possible)

The set of all permutations over the group formsunder : The set of all permutations over the group formsunder

Break-even point using break-even analysis : If we know that 20 people will attend, what price should be charged per person to break even?

E-business and e-commerce technologies : Describe the challenges e-Business and e-Commerce technologies present to the field of Information Technology.

Probability value on the marginal and joint probability : Find out the probability that a student from the whole school system, chosen at random, has passed?

Mechanical for full page : Briefly describe what would be found in a "mechanical" for a full page, full color magazine print ad-Finally, suggest a celebrity "spokesperson" that we could use in the ad, money is no object.

User Account

All Pages