The program is to print the time

Assignment Help Python Programming

Reference no: EM13158591

The Collatz sequence is the sequence of numbers generated by repeatedly computing the value of the function

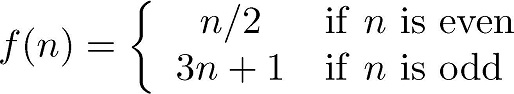
191_The program is to print the time.jpg

for n a positive integer, and stopping when n = 1.

So, for example, the Collatz sequence that begins with n = 6 is:

6, 3, 10, 5, 16, 8, 4, 2, 1

1.Write an iterative function itercol(n) that takes one argument, n,

and prints the Collatz sequence that begins withn.

itercol(6)

is to produce

6, 3, 10, 5, 16, 8, 4, 2, 1

2.Now write a recursive function reccol(n) that takes one argument, n,

 and prints the Collatz sequence that begins

 with n. Remember, this function must call itself! Also, you do not need

any loops - if you have one, you probably did it wrong.

reccol(6)

is to produce

6, 3, 10, 5, 16, 8, 4, 2, 1

Now you are to time the two functions and print out the timings. We will have to change your functions slightly to make the output manageable.

First, put both functions into a single file, and comment out the print statements in both functions. If you don't comment them out, you will get lots of output that you do not want.

Then, after the functions, read in the initial number for generating the sequences. Here, check that it is a positive integer. If it is not, give an error message and exit the program. (See below.)

Use the time.clock() function to time each function. To get a good value, call each function 10,000 times, noting the time before the calls and the time after the calls. Then divide the time by 10,000 to get the average time per call to the function. Print the average time the iterative function takes, the average time the recursive function takes, andwhich is faster and by how much (see below).

Input. Your program asks the user for a number, reads it in and checks that it is a positive integer, exiting with an error message if not.

Here is what a correct input should look like (the red text is what you type):

Compute the Collatz sequence for this number: 27

If the input is invalid:

Compute the Collatz sequence for this number: hello
Need a non-negative integer

and then the program exits.

Output. The program is to print the time in seconds that the iterative version takes, the time in seconds that the recursive version takes, and the difference between the times.

Your output for the input 27 should look exactly like this:

Average iterative Collatz time: 2.29415e-05 seconds
Average recursive Collatz time: 3.31636e-05 seconds
Iterative version is faster by 1.02221e-05 seconds

except that your times, which is faster, and the difference, may vary.

When printing the times, and the difference of the times, use the %g format (not the %e or %f formats). When printing which is faster, say "Iterative version is faster by ...", "Recursive version is faster by ...", or "Recursive and iterative versions are equally fast".

Reference no: EM13158591

Questions Cloud

Summarizes the topic argument of capital punishment : Post a brief statement that summarizes the topic argument of capital punishment, the type of argument that is being used and the sources that you are using to support your claims.

Explain why neanderthal groups in difference areas : Why might failure to specialize explain why Neanderthal groups in difference areas did not trade?

Ownership of the funds : What is your opinion as to whether the funds in the plan should be part of a company's financial balance sheet or a separate entity and not part of the company's financials? If they are part of the financials what is it saying as to the ownership ..

What is the volume of nitrogen at stp : A sample of nitrogen N2 has a volume of 300 mL at 34^C and a pressure of 745 mmHg. What is the Volume of Nitrogen at STP

The program is to print the time : The program is to print the time in seconds that the iterative version takes, the time in seconds that the recursive version takes, and the difference between the times.

What are the gains and losses of international trade : What are the gains and losses of international trade? What happens when tariffs are imposed, in terms of the importing and exporting countries? Use graphs as needed and explain your answers thoroughly.

Causes of world war first : List and adequately explain two causes of World War 1. When and why was the League of Nations created and what were its shortcomings?

How much of the salt would you need to add : If you had a saturated solution of NaNO3 at 40 degrees Celsius that contained 85 grams of water, how much of the salt would you need to add to have a saturated solution at 70 degrees Celsius?

Describe the details of tcr gene recombination : Overview the development process that yields a naive T lymphocyte. Do not describe the details of TcR gene recombination.

User Account

All Pages