Reference no: EM131112129

Our objectives are as follows:

1. Determine the effect of parameters on the solutions of differential equations.

2. Determine the behavior of the mass-spring system from the graph of the solution.

3. Determine the effect of the parameters on the behavior of the mass-spring. The primary MATLAB command used is the ode45 function.

1. From the graph in Fig. L5a answer the following questions.

(a) Which curve represents y = y(t)? How do you know?

(b) What is the period of the motion? Answer this question first graphically (by reading the period from the graph) and then analytically (by finding the period using ω₀).

(c) We say that the mass comes to rest if, after a certain time, the position of the mass remains within an arbitrary small distance from the equilibrium position. Will the mass ever come to rest? Why?

(d) What is the amplitude of the oscillations for y?

(e) What is the maximum velocity (in magnitude) attained by the mass, and when is it attained? Make sure you give all the t-values at which the velocity is maximum and the corresponding maximum value. The t-values can be determined by magnifying the MATLAB figure using the magnify button , and by using the periodicity of the velocity function.

(f) How does the size of the mass m and the stiffness k of the spring affect the motion?

Support your answer first with a theoretical analysis on how ω₀ - and therefore the period of the oscillation - is related to m and k, and then graphically by running LAB05ex1.m first with m = 5 and k = 4 and then with m = 1 and k = 16. Include the corresponding graphs.

2. The energy of the mass-spring system is given by the sum of the potential energy and kinetic energy. In absence of damping, the energy is conserved.

(a) Plot the quantity E = 1/2 mv² + 1/2 ky² as a function of time. What do you observe? Does the graph confirm the fact that the energy is conserved?

(b) Show analytically that dE/dt = 0.(Note that this proves that the energy is constant).

(c) Plot v vs y (phase plot). Does the curve ever get close to the origin? Why or why not? What does that mean for the mass-spring system?

3. Fill in LAB05ex1a.m to reproduce Fig. L5b and then answer the following questions.

(a) For what minimal time t₁ will the mass-spring system satisfy |y(t)| < 0.01 for all t > t₁? You can answer the question either by magnifying the MATLAB figure using the magnify button (include a graph that confirms your answer), or use the following MATLAB commands (explain):

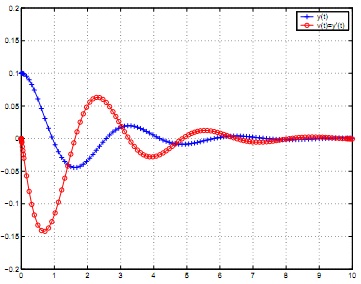
Figure L5b: Damped harmonic motion

for i=1:length(y)

m(i)=max(abs(y(i:end)));

end

i = find(m<0.01); i = i(1);

disp(['|y|<0.01 for t>t1 with ' num2str(t(i-1)) '<t1<' num2str(t(i))])

(b) What is the maximum (in magnitude) velocity attained by the mass, and when is it attained? Answer by using the magnify button and include the corresponding picture.

(c) How does the size of c affect the motion? To support your answer, run the file LAB05ex1.m for c = 2, c = 4, c = 6 and c = 8. Include the corresponding graphs with a title indicating the value of c used.

(d) Determine a nalytically the smallest (critical) value of c such that no oscillation appears in the solution.

4. (a) Plot the quantity E = 1/2 mv² + 1/2 ky² as a function of time. What do you observe? Is the energy conserved in this case?

(b) Show analytically that dE/dt < 0 for c > 0 while dE/dt > 0 for c < 0.

(c) Plot v vs y (phase plot). Comment on the behavior of the curve in the context of the motion of the spring. Does the graph ever get close to the origin? Why or why not?