Reference no: EM13974109
1. Section 11.3, Pages 516 - 517 # 9, 15, 16, 19, 20, 23, 24, 32, 35, 36, 41, 42 (Should read, "Repeat Problem 41"), 45, 46.
2. Section 11.4, Pages 525 - 526 # 1 - 4, 6, 7, 15, 16, 20 - 22, 27, 36, 37, 47, 48, 51, 52, 61 - 63, 65, 66, 70 - 72, 76 - 78.
3. Section 11.5, Pages 532 - 534 # 1 - 4, 6, 7, 11, 12, 19 - 22, 29, 30, 35, 36, 41 - 44, 56, 61, 67, 68, 70, 73, 74, 80 - 82.
4. Assume f and g are differentiable functions such that f(3) = 4, g(3) = 3, f′(3) = -6 and g′(3) = 5. For each of the following, evaluate the expression or determine that there is not enough information in the question to evaluate it:

5. Find the value of constants a, b and c such that the graph of the function y = ax2 + bx + c has x-intercepts of 0 and 5, and has a slope of 1 when x = 2.
6. Find the point(s) on the curve y = x + 1/x + 2 where the tangent line is parallel to the line y = 4x.
7. Suppose you work for a company where one of your responsibilities concerns the secure delivery of specialty computer parts from Scarborough to Kingston, Ontario. The delivery is made with an environmentally friendly truck whose ethanol consumption is described by the function
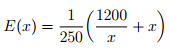
In this function, x represents the constant speed (in km/hr) at which the truck is driven and E(x) gives the gas consumption in litres/km. We assume x ≥ 5, the truck driver is paid $20 per hour to drive the 250 km from Scarborough to Kingston, and ethanol costs 80 cents per litre.
(a) Find the function C(x) that gives the total cost in dollars of the driver plus fuel for truck for the trip from Scarborough to Kingston.
(b) Find the marginal cost function when x = 75 and when x = 90.
(c) Calculate the speed (rounded to 1 decimal) at which the marginal cost function is equal to zero.
8. (This question is difficult !) Evaluate the following limits by interpreting them as the derivative of a certain function at a particular point (if you know l'Hopital's rule, do not use it):
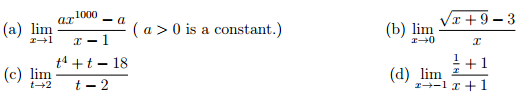
9. Find the equation of every line that has slope of -2 and is tangent to the curve y =1/x.
10. The quantity of expensive wristwatches demanded per month is related to their price by the equation
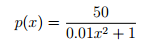
where p is measured in thousands of Canadian dollars per watch and x is the quantity of watches demanded, where 0 ≤ x ≤ 20.
(a) Find the revenue function, R(x)
(b) Find the marginal revenue function, R′(x).
(c) Compute R′(2) and interpret your result.
(d) Solve the equation R′(x) = 0.