Reference no: EM13920

Question 1)

1) Consider Efron's non-transitive dice where the 6 faces as are in the table below.

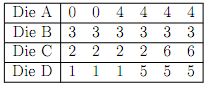
a) Suppose there are four players in the game and each will choose one die and roll it.The largest number will win. For each die, calculate the probability that the largest number observed occurs on that die. Which die would you choose?

b) Suppose there are four players in the game and each will choose one die and roll it. The person who rolls the smallest number will be eliminated. For each die, calculate the probability that the smallest number observed occurs on that die. Now which die would you choose (assuming you want to stay in the game rather than reading a good book, having root canal work, etc.)

c) Suppose that in the four player game, the person who rolls the smallest number pays $5.00 to the person who rolls the largest number. Calculate each player's expected gain after one round.

d) Suppose the person with die A loses the first round and is eliminated. The three players play another round with only dice B, C, and D. Again, the person who rolls the smallest number pays $5.00 to the person who rolls the largest number. Calculate each player's expected gain from this round.

e) Suppose the person with die D loses the first round and is eliminated. The three players play another round with only dice A, B, and C. Again, the person who rolls the smallest number pays $5.00 to the person who rolls the largest number. Calculate each player's expected gain from this round.

Question 2)

The probabilities for five discrete distributions that we have discussed can be computed recursively. In other words, if X is a random variable with probability function f_X(x)= P(X = x), then f_X(x)/f_X(x-1) = g(x), where g(x)may also contain parameters of the distribution ,and f_X(x-1) = 0. This can be a way to generate the probabilities in case functions like λn x " are not available. You start by computing P(X = minimum of the range of X) and get the rest recursively.

a) Find g(x)forthePoissondistributionwithparameter λ.

b) Find g(x)fortheBinomialdistributionwithparameters n and p.

c) Find g(x) for the Hypergeometric distribution with parameters a, b, n and N = a + b.

d) (Will this never end)fi Find g(x) for the Negative Binomial distribution for X, the number of trials until the rth success in a sequence of Bernoulli trials with P(S)= p.

Question 3)

For a research study on smoking cessation, we need a sample of 25 smokers from a population of 24,000 undergraduates. Assume there are 2,880 smokers and 21,120 non-smokers in the population.

a) Let X be a random variable giving the number of smokers in a simple random sample of 200 from the population (chosen without replacement, of course). Give an expression for P(X =25).

b) Suppose we want to sample until we have obtained 25 smokers. Let Y be a random variable giving the number of people we must sample (without replacement) to obtain 25 smokers. Give an expression for P(Y =220).

c) Stratified Random Sample In the 24,000 people in the population, there are 14,000 males of whom 1920 smoke, and 10,000 females of whom 960 smoke. We decide to take a sample of 120 males and 80 females (at random without replacement). Let Z_M and Z_F be random variables giving the number of male smokers and female smokers in the sample. Give an expression for P(Z_M + Z_F = 25).

d) Suppose we do the stratified random sampling as in c). If our sample contains 25 smokers, what is the probability that 14 of the smokers will be malesfi An expression is fine here.

Question 4)

The safe level of total coliform bacteria in well water is 5 or fewer bacteria per 100 ml. Then one rule for declaring a sample to be "safe" is if a 20 ml sample contains 0 or 1 bacteria. Assume coliform bacteria in well water are distributed according to a Poisson process at an average concentration of λ per 100 ml, and let X be a random variable giving the number of coliform bacteria in a 20 ml sample of well water.

a) If λ = 10 (twice the safe limit), what is the probability a 20 ml test tube will contain 0 or 1 bacteria (and so the sample will be declared "safe")?

b) Regulations require that three consecutive samples taken one week apart all have to be "safe" in order to declare the well "safe". If λ =10 each week, what is the probability that all three 20 ml samples will show 0 or 1 bacteria?

c) A 200 ml container is used to collect a larger sample and this sample is transferred to ten 20 ml test tubes for analysis. If λ =10 and the 200ml sample contains 20 bacteria,derive the probability distribution for Y , the number of bacteria in the first test tube. Name the probability distribution for Y ,andgive E(Y )and V ar(Y ).

d) The regulators feel that the current regulations requiring 3 safe samples taken a week apart are not protective enough if λ =10.They are thinking of changing the rules to either defining a safe sample as one with 0 bacteria and requiring a safe sample each week for three weeks, or keeping the definition of a safe sample as it is but requiring a safe sample each week for n weeks. Find the smallest value of n so that, if λ =10, P(declare a sample safe under Rule 2) <P(declare a sample safe under Rule 1)