Stephanie the human cannonball will be fired from a cannon

Reference no: EM13373164

Stephanie the Human Cannonball will be fired from a cannon and hopes to and in a small net at the opposite end of the circus arena. Your job as Stephanie's manager is to do the mathematical calculations that will allow Stephanie to perform her death defying act safely. The methods that you will use are from the field of ballistics (the study of projectile motion).

The Problem

Stephanie's cannon has a muzzle velocity of 35m/s, which means that Stephanie will leave the muzzle with that velocity. The muzzle opening will be 5m above the ground and Stephanie's objective is to land in a net that is also 5m above the ground and that extends a distance of 10m. (Figure 1).

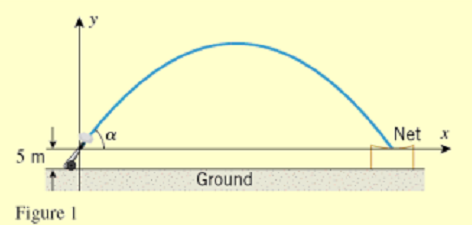
246_Determine the elevation angle.png

Before solving the problem you must clearly state any assumptions that you will be using to establish your model.

Question 1

The horizontal range R of a particle is the horizontal distance travelled when the particle returns to ground level.

(a) Algebraically Show that

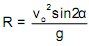
(b) Determine the elevation angle that will produce the maximum range?

(c) Algebraically and graphically, find the maximum distance that the net can be from the cannon. The ring announcer would also like to know how long Stephanie will be in the air and the maximum height she will achieve.

Question 2

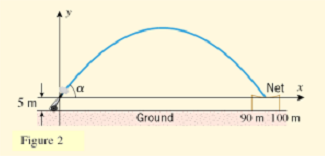
1461_Determine the elevation angle2.png

The net has been placed so that its middle is 95m away from the cannon. (Figure 2). The circus is being held inside a large tent with a flat ceiling 45m high. Can Stephanie be fired to the net without striking the ceiling? If so, what should the cannon's angle of elevation be?

Question 3

Stephanie decides to raise the net to 20m above the ground. What is the maximum distance that the net can be placed from the cannon? At what angle of launch will this be achieved?

Question 4

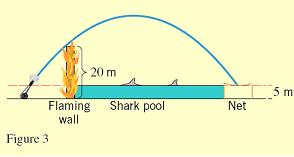
For her final act, Stephanie is to be fired from 5m above ground level with a muzzle velocity of 35m/s over a flaming wall that is 20m high and past a 5m high shark pool (Figure 3). To make the feat impressive, the pool will be made as long as possible. Your job as Stephanie's manager is to determine the length of the pool, how far to place the cannon from the wall and what elevation angle to use
to ensure that Stephanie clears the pool.

2488_Determine the elevation angle3.png

Question 5

Which is Faster, Going Up or Coming Down?

Suppose you throw a 1kg ball into the air. Determine whether the ball takes longer to reach its maximum height or fall back to Earth from its maximum height?

Assume the forces acting on the ball are the force of gravity and a retarding force of air resistance with direction opposite to the direction of motion. (-mkv) (assume k = 0.1)

Question 6

Stephanie claims that your model is fundamentally flawed.

Extend and refine your model to make it more realistic.

Clearly state any assumptions you used to create your model.

Discuss the effect of your new assumptions on Stephanie's flight path.

Reference no: EM13373164

Questions Cloud

Question a corporation had stockholders equity on january 1 : question a corporation had stockholders equity on january 1 as follows common stock 5 par value 1000000 shares

Part one international and comparative law with regard to : part one international and comparative law with regard to the relationship between treaties and australian law campbell

Please need presentation about diversity management the : please need presentation about diversity management. the topics you have to concentrate about1.pros and cons of

Business ethics decision making for personal integrity amp : business ethics decision making for personal integrity amp social responsibility second edition by laura p. hartman and

Stephanie the human cannonball will be fired from a cannon : stephanie the human cannonball will be fired from a cannon and hopes to and in a small net at the opposite end of the

Do students at various universities differ in how sociable : do students at various universities differ in how sociable they are? twenty-five students were randomly selected from

Question 1nbsp the johnson corporation is authorized to : question 1nbsp the johnson corporation is authorized to issue 3000 shares of 8 percent 50 par-value preferred stock

Jordana woolens is a manufacturer of wool cloth the : jordana woolens is a manufacturer of wool cloth. the information for march is as follows beginning work-in-process

The logistics company tlclogistics planning project : the logistics company tlclogistics planning project ideabackground and justificationthe logistics company tlc has been

User Account

All Pages