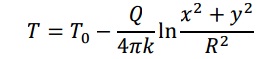Reference no: EM13865294

1. The stationary heat-conduction problem is governed by Poisson's equation (in 2D Cartesian coordinates):

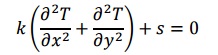
Consider the stationary heat condution in a uniform circular disk of radius ?? = 5 cm and thickness 1 mm. The disk is made of aluminum with thermal conductivity ?? = 200 W m · K ⁄ . The plate is being heated with a uniformly distributed volumetric heat source ?? = 10 kW m3 ⁄ . The perimeter of the disk is held at constant temperature ??0 = 20?.

1) Utilize the symmetry of the problem and solve the equation on a quarter of the disk, what boundary conditions needs to be applied on the symmetry lines?

2) Convert the partial differential equation and the natural boundary conditions to a weak form, and state the essential boundary conditions (if any).

3) Implement the weak form in COMSOL by using the 2D weak-form module in a stationary mode. Use triangular and quadrilateral elements in both linear and quadratic orders, study the convergence and mesh dependence. Discuss your observation. (You may use the L2 error

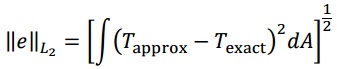
The exact solution of the equation is

4) Select one case (with the largest elements you used), and generate the 2D plot of the error distribution of the heat flux: qx = -k ??t ???? ⁄ , ???? = -?? ???? ???? ⁄ . Where are the flux results more accurate?

2. Now consider the heat conduction on the same disk, but instead of the distributed heat source s, there is a concentrated source ?? = 100??/?? located on the central axis of the disk.

1) How would the weak-form equation change? (Hint: consider a distributed source only on part of the disk, and then take the limit and let the volume/area of the part go to infinitesimal.)

2) Repeat question 3) of Problem 1. Now the exact solution is