Reference no: EM131060
A consumer products company wants to calculate the effectiveness of different types of advertising media in the promotion of its products. Specially, two kind of advertising media are to be considered: radio and television advertising and newspaper advertising (including the cost of discount coupons). A sample of 22 cities with approximately equal population is selected for study during a test period of one month. Each city is allocated a specific expenditure level both for radio and television advertising and for newspaper advertising. The sales of the product (in thousands of dollars) and also the levels of media expenditure (in thousands of dollars) during the test month are recorded, answer the following:
a) State the multiple regression equation.
b) Interpret the meaning of the slopes b1 and b2 in this problem.
c) Interpret the meaning of the regression coefficient b0 in this problem.
d) Predict the average sales for a city in which radio and television advertising is $20,000 and newspaper advertising is $20,000.
e) Set up a 95% confidence interval estimate for the average sales for cities in which radio and television advertising is $20,000 and newspaper advertising is $20,000.
f) Set up a 95% confidence interval estimate for the sales for an individual city in which radio and television advertising is $20,000 and newspaper advertising is $20,000.
g) Determine whether there is a significant relationship between sales and the two independent variables (radio advertising and newspaper advertising) at the 0.05 level of significance.
h) Interpret the meaning of the p-value.
i) Determine the coefficient of multiple determination, r2.
j) Determine the adjusted r2.
k) Perform a residual analysis on your results and determine the adequacy of the fit of the model.
l) Set up a 95% confidence interval estimate of the population slope between sales and radio and television advertising.
m) At the 0.05 level of significance, determine whether each explanatory variable makes a significant contribution to the regression model. On the basis of these results, indicate the independent variables that should be included in this model.
n) Compute the coefficients of partial determination, r2Y1.2.and r2Y2.1.and interpret their meaning.
A collector of antique grandfather clocks believes that the price (in dollars) received for the clocks at an antique auction increases with the age of the clocks and with the number of bidders. Thus the model is hypothesized is
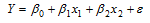where y = auction price, x1 = age of clock (years) and x2 = number of bidders.
A sample of 32 auction prices of grandfather clocks, along with their ages and the number of bidders, is given below (clock_bidders.xls).
|
Age (x1)
|
Bidders (x2)
|
Price (y)
|
Age (x1)
|
Bidders (x2)
|
Price (y)
|
|
127
|
13
|
1235
|
170
|
14
|
2131
|
|
115
|
12
|
1080
|
182
|
8
|
1550
|
|
127
|
7
|
845
|
162
|
11
|
1884
|
|
150
|
9
|
1522
|
184
|
10
|
2041
|
|
156
|
6
|
1047
|
143
|
6
|
854
|
|
182
|
11
|
1979
|
159
|
9
|
1483
|
|
156
|
12
|
1822
|
108
|
14
|
1055
|
|
132
|
10
|
1253
|
175
|
8
|
1545
|
|
137
|
9
|
1297
|
108
|
6
|
729
|
|
113
|
9
|
946
|
179
|
9
|
1792
|
|
137
|
15
|
1713
|
111
|
15
|
1175
|
|
117
|
11
|
1024
|
187
|
8
|
1593
|
|
137
|
8
|
1147
|
111
|
7
|
785
|
|
153
|
6
|
1092
|
115
|
7
|
744
|
|
117
|
13
|
1152
|
194
|
5
|
1356
|
|
126
|
10
|
1336
|
168
|
7
|
1262
|
a) State the multiple regression equation.
b) Interpret the meaning of the slopes b1 and b2 in the model.
c) Interpret the meaning of the regression coefficient b0.
d) Test H0: b2 = 0 against H1: b2 0. Interpret your finding.
e) Use a 95% confidence interval to estimate b2. Interpret the p-value corresponding to the estimate b2. Does the confidence interval support your interpretation in d)?
f) Determine the coefficient of multiple determination r2 and interpret its meaning.
g) Perform a residual analysis on your results and determine the adequacy of the fit of the model.
h) Plot the residuals against the prices. Is there evidence of a pattern in the residuals? Explain.
i) At a = 0.05, is there evidence of positive autocorrelation in the residuals?
j) Suppose the collector, having observed many auctions, believes that the rate of increase of the auction price with age will be driven upward by a large number of bidders. In other words, the collector believes that the age of clock and the number of bidders should interact. Is there evidence to support his claim that the rate of change in the mean price of the clocks with age increases as the number of bidders increases? Should the interaction term (x1x x2) be included in the model? If so, what is the multiple regression equation?