Reference no: EM13927308

Function [x] = gaussel(A,b)

% [x] = gaussel(A,b)
%
% This subroutine will perform Gaussian elimination
% and back substitution to solve the system Ax = b.
% INPUT : A - matrix for the left hand side.
% b - vector for the right hand side
%
% OUTPUT : x - the solution vector.
N = max(size(A));
% Perform Gaussian Elimination
for j=2:N,
fori=j:N,
m = A(i,j-1)/A(j-1,j-1);
A(i,:) = A(i,:) - A(j-1,:)*m;
b(i) = b(i) - m*b(j-1);
end
end
% Perform back substitution
x = zeros(N,1);
x(N) = b(N)/A(N,N);
for j=N-1:-1:1,
x(j) = (b(j)-A(j,j+1:N)*x(j+1:N))/A(j,j);
end

% End of function

a)The above programme solves a linear system of equations using naïve Gaussian elimination.

Modify this programme so that it outputs upper and lower triangular matrices of LU factorisation. The header line of the modified function should read [x, L, U] = gaussel(A, b)

Use this function, to solve the system Ax = b, where

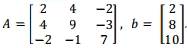
b) Use the LU factorisation of A obtained above to solve the system Ax = c, where

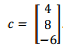
You can use the ‘backslash' Matlab operator for solving the systems of equations with L and U.