Reference no: EM13974176

Linear Programming Problem

Max { z = 4x1 + x2 + 5x3 + 3x4 }  subject to constraints:
x1 - x2 - x3 + 3x4 ≤1;
5 x1 + x2 + 3x3 + 8x4 ≤ 55;
-x1 + 2x2 + 3x3 - 5x4 ≤ 3;
xj ≥ 0, j = 1, 2, 3, 4.

Solve the above problem using Simplex algorithm, show all iterations, then compose the corresponding dual problem and apply results of the Duality Theory to the dual pair.

1) Simplex solution: Introducing 3 more variables ( x5, x6, x7 ) to equalize the constraints we get:

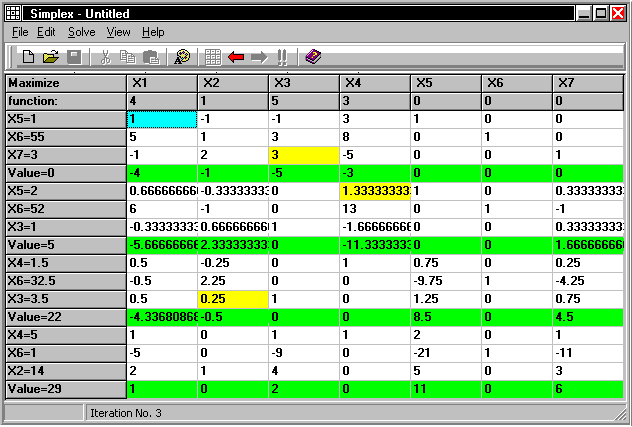
The simplex solution in 3 iterations is shown above. The optimal solution: 

z_max = 29, x1 = 0, x2 = 14, x3 = 0, x4 = 5 ( x5 = 0, x6 = 1, x7 = 0 )

2) The dual problem: We have a symmetric dual pair since in the original all constraints are inequalities ("≤ " in max-problem) with non-negative variables, hence the dual variables (y1, y2, y3) are also non-negative and all constraints should be inequalities ("≥" in min-problem). The matrices of both problems are transposed (so min-problem will have 4 constraints with 3 variables). Finally the object function coefficients in each problem become right hand sides in the dual and vice versa:

Min { w = y1 + 55y2 + 3y3 }  subject to constraints:

y1 + 5y2 - y3 ≥ 4;
-y1 + y2 + 2y3 ≥ 1;
-y1 + 3y2 + 3y3 ≥ 5;
3y1 + 8y2 - 5y3 ≥ 3;
yi≥ 0, i = 1, 2, 3.

3) Optimal solutions for the dual pair: According the Duality Theory in Linear Programming the optimal simplex tableau of the primal problem provides the optimal solution of the dual also: take the final Δj,  j = 5, 6, 7, corresponding to variables from the initial basis (x5, x6, x7) and add their object coefficients (all c5, c6, c7 are 0 here)

y1 = Δ₅ + c₅ = 11 + 0 = 11; y₂ = Δ₆ + c₆ = 0 + 0 = 0;  y₃ = Δ₇ + c₇ = 6 + 0 = 0

For (y₁, y₂, y₃ ) = (11, 0, 6) we have w_min = 11 + 55*0 + 3*6 = 29 = z_max as proven in the Main Duality Theorem.

For the optimal solution X_max = (0, 14, 0, 5) we have:
0 - 14 - 0 + 3*5 = 1, so the 1st constraint is satisfied exactly;
5*0 + 14 + 3*0 + 8*5 = 54 < 55, so the 2nd constraint is not satisfied exactly (x6 = 1 > 0), hence y2 = 0 in Y_min;
-0 + 2*14 + 3*0 - 5*5 = 3, so the 3^rd constraint is satisfied exactly;
Also 2nd and 4th components in X_max being positive means that 2nd and 4th dual constraints are satisfied exactly.

For the optimal solution Y_min = (11, 0, 6) the 1st and 3rd constraints are not satisfied exactly, hence in the optimal solution of the primal x1 = x 3 = 0; 1st and 3rd components being positive implies the corresponding constraints in the max-problem to be satisfied exactly, as shown above.