Reference no: EM13551203
(a) Show that if y = f(x) is a solution to the differential equation dy/dx = 3y2/3 that is not zero on an open interval I, then on this interval f(x) must be of the form
f(x) = (x - c)3 for some constant c not in I.
(b) Prove that if y = f(x) is a solution to the differential equation dy/dx = 3y2/3 on (-∞, +∞) and f(a) = f(b) = 0, where a < b, then f(x) = 0 for a ≤ x ≤ b.
(c ) Now let y = g(x) be a solution to the IVP (7) on ( -∞, +∞). Of course g(2) = 0. If g vanishes at some point x > 2, then let b be the largest of such points; otherwise, set b = 2. Similarly, if g vanishes at some point x < 2, then let a be the smallest (furthest to the left) of such points; otherwise, set a = 2. Here we allow b = +∞ and a = -∞. (Because g is a continuous function, it can be proved that there always exist such largest and smallest points.) Using the results of parts (a) and (b) prove that if both a and b are finite, then g has the following form:
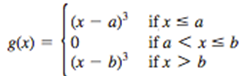
What is the form of g if b = +∞? If a = -∞? If both b = +∞ and a = -∞?
(d) Verify directly that the above concatenated function g is indeed a solution to the IVP (7) for all choices of a and b with a ≤ 2 ≤ b. Also sketch the graph of several of the solution function g in part (c) for various values of a and 12, including infinite values.